OSK SMP 2024 – JELAJAH NALAR

Atlet bulu tangkis Anthony Ginting menjalani pertandingan persahabatan dengan Jonathan Christie, rekan sesama timnya. Pertandingan berakhir jika salah satu pemain menang dua set langsung atau mennag dua set dari tiga set permainan (rubber set). Tim pelatih Ginting menyatakan bahwa peluang ginting dapat memenangkan suatu set adalah 1,6 kali lipat peluang Ginting memenangkan pertandingan. Misalkan tidak ada pertandingan yang berakhir imbang/seri. Berdasarkan pernyataan tim pelatih Ginting, peluang Jonathan memenangkan pertandingan adalah …
A. $\frac{1}{4}$
B. $\frac{3}{4}$
C. $\frac{5}{32}$
D. $\frac{27}{32}$
Diketahui sistem persamaan sebagai dengan $a, b$ dan $c$ adalah bilangan real positif. $$a=bc$$ $$b=c(a+2)$$ $$c=b(a-2)$$ Nilai dari $a^{2}+b^{2}+c^{2}$ adalah …
A. 15
B. $15-4\sqrt{5}$
C. 225
D. $15+4\sqrt{5}$
Diketahui suatu kerucut dengan titik puncak $T$, pusat sisi alas $O$ dan diameter alas $AB$. Titik $C$ berada pada ruas garis $AT$ dengan $AC=OC=11$ cm. Titik $D$ merupakan titik potong antara garis $OT$ dan $BC$ dengan $DC=7$ cm. Volume kerucut tersebut adalah … $cm^{2}$.
A. 196$\pi$
B. 960$\pi$
C. 1960$\pi$
D. 9600$\pi$
Misalkan $N(a,b,c)$ menyatakan banyaknya kelipatan $a$ yang lebih besar dari $b$ dan kurang dari $c$. Sebagai contoh, $N(3,5,10)=2$ karena terdapat dua bilangan antara 5 dan 10 yang merupakan kelipatan 3. Nilai dari $N(6^{4},6^{4},6^{6})$ adalah …
A. 216
B. 215
C. 209
D. 208
Perhatikan gambar berikut.

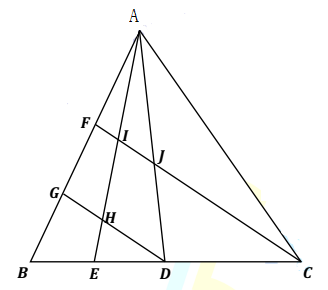
Diketahui panjang $BD=CD,BE=DE,AJ=JD$ dan $DG$ sejajar $CF$. Jika perbandingan luas daerah segitiga $ADH$ dan segitiga $ABC$ dinyatakan dalam bentuk paling sederhana $m:n$, maka nilai $m+n$ adalah …
A. 5
B. 6
C. 7
D. 8
Jika $x^{3}+\frac{1}{x^{3}}=18$ dan $x\neq 0$, maka nilai dari $$x^{7}+\frac{1}{x^{7}}+7$$ adalah …
A. 845
B. 850
C. 855
D. 860
Suatu segi delapan $ABCDEFGH$ dibentuk dari suatu persegi $ABCD$ dan persegi panjang $EFGH$ yang panjang sisi-sisinya merupakan bilangan bulat positif. Contoh segi delapan tersebut diberikan pada gambar berikut.

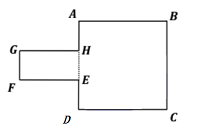
Jika luas persegi adalah x $cm^{2}$, luas persegi panjang adalah y $cm^{2}$, $x>y$ dan $xy=98$, maka keliling segi delapan $ABCDEFGH$ yang mungkin adalah … cm.
A. 30
B. 33
C. 34
D. 51
Jika bilangan real positif $p,q,r,s$ memenuhi sistem persamaan $$p^{2}+q^{2}=r^{2}+s^{2},$$ $$p^{2}+s^{2}-ps=q^{2}+r^{2}+qr,$$ Nilai dari $$\frac{pq+rs}{ps+qr}$$ adalah …
A. $\frac{\sqrt{2}}{3}$
B. $\frac{\sqrt{2}}{2}$
C. $\frac{\sqrt{3}}{3}$
D. $\frac{\sqrt{3}}{2}$
Suatu bilangan bulat positif $n$ disebut bilangan JUMPAT jika jumlah $n$ bilangan bulat positif pertama dapat dinyatakan sebagai penjumlahan empat bilangan bulat positif berurutan. Banyaknya bilangan JUMPAT yang kurang dari 2024 adalah …
A. 252
B. 253
C. 504
D. 505
Diketahui persamaan $$x^{4}+ax^{3}+54x^{2}-108x+81=0$$ dengan $a$ bilangan real, memiliki 4 akar real berbeda, yaitu $r_{1},r_{2},r_{3},r_{4}$. Jika $$r_{1}\text{ x }r_{2}\text{ x }r_{3}\text{ x }r_{4}=\left( \frac{r_{1}+r_{2}+r_{3}+r_{4}}{4}\right)^{4}$$ maka nilai dari $a$ adalah …
A. -12
B. -8
C. 3
D. 12
Sepuluh persegi panjang kecil dengan ukuran 1 cm x 2 cm akan digunakan untuk membentuk persegi panjang besar dengan ukuran 10 cm x 2 cm. Banyaknya cara membentuk persegi panjang besar tersebut adalah …
Keterangan: Berikut adalah beberapa contoh cara membentuk persegi panjang besar yang mungkin untuk dilakukan.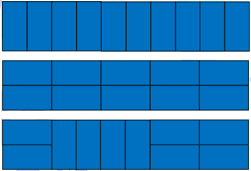

A. 78
B. 89
C. 144
D. 233
Diketahui segitiga sama kaki $ABC$ dengan $AB=BC=8$ cm dan $\angle ABC=120\circ$. Titik tengah $AB$ dan $BC$ masing-masing adalah $D$ dan $E$. Garis $DF$ tegak lurus $AB$ dan $EF$ tegak lurus $BC$. Luas daerah yang diarsir adalah … $cm^{2}$.

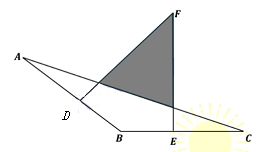
A. $\frac{8}{3}\sqrt{3}$
B. $\frac{16}{3}\sqrt{3}$
C. $8\sqrt{3}$
D. $16\sqrt{3}$
Dari segilima $ABCDE$ dipilih 21 titik yang berbeda. Satu titik dari sisi $AB$, dua titik dari sisi $BC$, tiga titik dari sisi $CD$, empat titik dari sisi $DE$, lima titik dari sudut $A, B, C, D, E$ dan enam titik dari sisi $AE$. Banyaknya segitiga yang dapat dibentuk dari seluruh titik yang dipilih adalah …
A. 560
B. 770
C. 1239
D. 1330
Diketahui $x$ merupakan bilangan bulat positif kelipatan 2 yang kurang dari 50, $y$ merupakan bilangan bulat positif kelipatan 3, dan $y-x=10$. Jika $A$ adalah himpunan semua faktor prima dari $x, B$ adalah himpunan semua faktor prima dari $y$, dan jumlah semua anggota dari $Acup B$ adalah 10, maka nilai dari $x+y$ adalah …
A. 14
B. 26
C. 38
D. 50
Gina bermain angka dengan mengisikan bilangan bulat 1, 2, …, 9 pada tabel 3 x 3. Sehingga, hasil kali ketiga bilangan pada setiap baris adalah bilangan yang terdapat dikanan tabel dan hasil kali ketiga bilangan pada setiap kolom adalah bilangan yang terdapat dibawah tabel, seperti terlihat sebagai berikut.

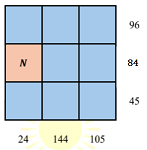
Nilai $N$ adalah …
A. 1
B. 3
C. 4
D. 6
Sekelompok bilangan berbeda terdiri dari 6 bilangan genap dan 4 bilangan ganjil. Dari kelompok bilangan tersebut diperoleh informasi sebagai berikut.
- Jangkauan data = 24
- Jangkauan antar kuartil = 14
- Bilangan ke-3, 5, 6 dan 8 adalah bilangan ganjil
- Median = 2024
- Rata-rata bilangan ganjil adalah 2022
Rata-rata terbesr yang mungkin dimiliki oleh kelompok bilangan tersebut adalah …
A. 2022
B. 2022,4
C. 2024
D. 2024,4
Jumlah semua bilangan ratusan yang ketiga digitnya berbeda dan tidak memuat 0 adalah …
A. 359.640
B. 279.720
C. 277.200
D. 252.000
Diberikan 4 bola pejal berukuran sama dengan diameter 22 cm dan sebuah silinder dengan diameter 46 cm. Dua bola diletakkan di dasar silinder dengan jarak pusat keduanya 24 cm. Dua bola sisanya juga dimasukkan ke dalam silinder dengan jarak antar pusat keduanya 24 cm dan garis yang menghubungkan kedua pusat bola ini tegak lurus dngan garis yang menghubungkan kedua pusat bola sebelumnya. Jika air dimasukkan kedalam silinder sehingga menutupi seluruh bola, maka volume minimum air yang dimasukan adalah … $cm^{3}$.
A. $307\frac{1}{3}\pi$
B. $529\frac{1}{3}\pi$
C. $1694\pi$
D. $7098\frac{2}{3}\pi$
Empat bilangan asli kurang dari sepuluh memiliki rata-rata, median dan modus tunggal yang membentuk tiga bilangan asli berurutan. Jika $A$ adalah jumlah terkecil yang mungkin dari empat bilangan tersebut dan $B$ adalah jumlah terbesar yang mungkin dari empat bilangan tersebut, maka nilai dari $A+B$ adalah …
A. 36
B. 40
C. 42
D. 44
Bilangan-bilangan 4, 5, 6, 9, 11, 12, 18, 20 dan 24 akan diletakkan pada 4 lingkaran dan 5 persegi yang disusun dalam satu baris sebagai berikut.

Setiap bilangan harus digunakan tepat satu kali dan diletakkan di tempat yang berbeda. Selain itu, bilangan pada setiap lingkaran harus merupakan hasil penjumlahan dari dua bilangan pada persegi yang berada tepat disebelah kiri dan kanannya. Jika $x$ adalah bilangan pada persegi paling kiri dan $y$ adalah bilangan pada persegi paling kanan, maka nilai terbesar yang mungkin dari $x+y$ adalah …
A. 32
B. 38
C. 42
D. 44
Diketahui $A=\{0, 1, 2, …, 9\}$ dan $\overline {rstu}$ adalah bilangan empat digit dengan $r, s, t, u$ adalah anggota $A$ yang berbeda. Jika $\overline {rstu}+\overline {stu}=\overline {vwxyz}$, dengan $r, s, t, u, v, w, x, y, z$ adalah anggota $A$ yang berbeda, maka anggota $A$ yang tidak digunakan dalam operasi penjumlahan tersebut adalah …
A. 2
B. 3
C. 5
D. 8
Banyaknya faktor dari 2024 yang lebih besar dari $\sqrt{2024}$ adalah …
A. 4
B. 8
C. 12
D. 16
Diketahui pertidaksamaan $$\sqrt{x-3}+\sqrt{6-x\ge p}$$ memiliki penyelesaian untuk $x\in \mathbb{R}$. Nilai $p$ terbesar yang mungkin adalah …
A. $\sqrt{6}$
B. 3
C. $\sqrt{6}+\sqrt{3}$
D. 6
Segi enam beraturan $ABCDEF$ memiliki panjang sisi 2024 mm. Titik $G$ adalah titik tengah $AB$ dan titik $H$ adalah titik tengah $EG$. Perbandingan luas daerah segitiga $CDH$ dan segi enam $ABCDEF$ adalah …
A. 4 : 24
B. 5 : 24
C. 6 : 24
D. 7 : 24
Diketahui $a,b$ dan $c$ adalah bilangan ratusan yang satuannya sama dengan ratusannya. Jika $b=2a+1$ dan $c=2b+1$, maka banyaknya kemungkinan tripel $(a, b, c)$ yang berbeda adalah …
A. 1
B. 2
C. 3
D. 4