Tenda A dan tenda B seperti dalam gambar memiliki lebar 3 m dan tinggi 2m. Luas bahan yang digunakan untuk membuat tenda A dan tenda B sama. Jika panjang tenda A adalah 6 m, maka nilai p sama dengan …
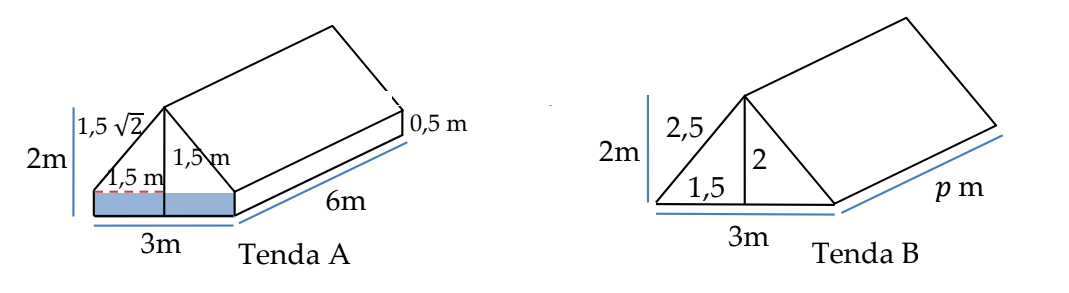A. $\frac{3}{2}+4\sqrt{2}$B. 6C. $\frac{3}{2}+\frac{18}{5}\sqrt{2}$D. 8- Misalkan $(p, q, r, s)$ adalah pasangan 4 bilangan dari himpunan (2,3,4,5) yang tidak harus berbeda sehingga $p × q − r × s$ adalah bilangan ganjil. Banyaknya pasangan bilangan yang memenuhi adalah …A. 48B. 64C. 96D. 128
- Diketahui persamaan kuadrat $ax^{2} + bx + c = 0$ tidak mempunyai akar bilangan real, tetapi Dina mendapatkan akar −3 dan −6 karena salah menulis nilai dari $a$. Sedangkan Toni mendapatkan akar −1 dan 2 karena salah menuliskan tanda dari $a$. Nilai dari $\frac{3b+4c}{a}$ adalah …A. -5B. 5C. 8D. 11
- Perbandingan panjang kaki sudut siku-siku sebuah segitiga siku-siku adalah 2 : 3. Jika panjang sisi miring segitiga tersebut $5\sqrt{13}$, maka luas segitiga siku-siku tersebut adalah …A. 12B. 27C. 48D. 75
- Hasil kali tiga bilangan bulat positif yang berurutan adalah enam belas kali hasil penjumlahan ketiga bilangan tersebut. Jumlah kuadrat bilangan tersebut adalah …A. 21B. 149C. 194D. 441
- Diketahui $xy = 15$ dan $(2x − y)^{4} = 1$. Misalkan $z$ adalah jumlah dari kuadrat semua nilai $y$ yang mungkin, maka $z$ = …A. 0B. 30,5C. 100D. 122
- Suatu system pencatat kuantitas stok otomatis mengalami gagal desain yang cukup fatal, yaitu tidak terdefinisinya angka 4 dan 6 di system tersebut. Jadi, setelah menampilkan 3, system akan menampilkan 5 dan setelahnya 7. Hal ini terjadi untuk seluruh nilai tempat. Sehingga, setelah menampilkan 399, system akan menampilkan 500 sebagai nilai selanjutnya. Jika system tersebut menyampaikan bahwa tersedia stok tepung sebanyak 1578 bungkus, maka banyak stok tepung yag sesungguhnya tersedia adalah … bungkus.A. 814B. 896C. 1456D. 1467
- Lima data bilangan asli tidak lebih dari sepuluh mempunyai modus 5 dan rata-rata 6. Jika terhadap lima data tersebut ditambah satu data bilangan asli yang tidak lebih dari 10, maka salah satu median yang mungkin dari enam data adalah …A. 4B. 4,5C. 5D. 6,5
- Sebuah bilangan bulat yang terdiri atas empat digit akan disusun sedemikian sehingga berupa bilangan genap dengan digit pertama (paling kiri) bernilai genap serta tidak ada angka yang berulang. Banyaknya cara menyusun bilangan tersebut adalah …A. 120B. 896C. 1120D. 5040
Perhatikan gambar. Setiap 12 menit Bus-A dapat menempuh rute P-X-S-X-P. Setiap 20 menit, Bus-B dapat menyelesaikan rute Q-X-T-X-Q. Setiap 28 menit Bus-C dapat menyelesaikan rute R-X-U-X-R. Pukul 1 siang (13.00), Bus-A berangkat dari P, Bus-B berangkat dari Q, dan Bus-C berangkat dari R, menempuh rutenya masing-masing dengan kecepatan konstan dan mengulangi perjalanan sepanjang rutenya hingga pukul 11 malam (23.00). Diantara pukul 5 sore hingga pukul 10 malam (17.00 – 22.00), berapa kali 2 atau lebih bus tiba di X secara bersamaan?
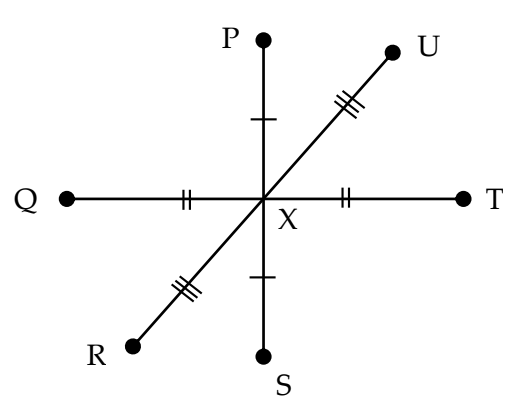A. 18B. 19C. 20D. 21- Misalkan bilangan pecahan $\frac{27}{5}$ dapat dinyatakan sebagai $$\frac{27}{5}=A+\frac{1}{B+\frac{1}{C+1}}$$ dengan $A, B, C$ adalah bilangan bulat. Nilai $A$ x $B$ x $C$ adalah …A. 9B. 10C. 15D. 20
- Di suatu fasilitas kesehatan, empat pasang suami istri sedang mengantri untuk disuntik vaksin satu per satu. Jika setiap suami menghendaki istrinya untuk disuntik terlebih dahulu daripada dirinya dan setiap pasang suami istri tidak harus disuntik berurutan, banyak urutan penyuntikan vaksin berbeda yang mungkin adalah …A. 24B. 576C. 2520D. 40260
- Pada $\Delta ABC, \angle ACB = 120°$. Titik $E$ dan $F$ berturut-turut berada pada sisi $AB$ dan $AC$. Jika $AF = FE = EC = CB$, maka $\angle ABC$ = …A. 15°B. 30°C. 36°D. 45°
Sebuah lantai berbentuk persegi dilapisi dengan ubin berbentuk persegi dengan panjang sisi $p$ satuan sebanyak $n$ buah. Untuk $n = 4$ dapat dilihat seperti gambar berikut. Diketahui $q$ adalah jarak antar ubin pada satu baris dan kolom serta jarak ubin terluar dengan sisi lantai. Jika $n = 81$ maka persentase luas seluruh ubin dibandingkan luas lantai adalah 64%. Perbandingan nilai $p$ dan $q$ adalah …
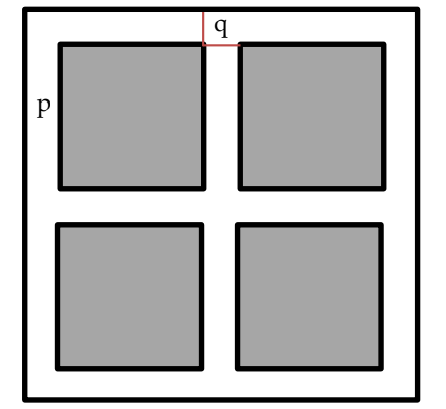A. 40 : 9B. 40 : 3C. 8 : 6D. 8 : 3- A mendapat giliran ronda malam setiap 4 hari, B mendapat giliran ronda setiap 5 hari, dan C mendapat giliran ronda setiap 6 hari. Jika A dan B muai ronda bersama pada tanggal 1 Januari 2021, sedangkan C ronda dua hari kemudian, maka mereka bertiga akan ronda bersama-sama untuk ke-3 kalinya pada tanggal …A. 1 Mei 2021B. 3 Mei 2021C. 21 Mei 2021D. 23 Mei 2021
- P adalah titik minimum grafik fungsi kuadrat yang melalui (2a, 0), (4a, 0), dan (0, 3a) dengan a > 0. Agar jarak $P$ ke sumbu-x lebih dari 3 satuan, maka nilai a adalah …A. 0 < a < 3B. 0 < a < 8C. a > 3D. a > 8
- Diketahui koordinat titik $A$ dan $B$ berturut-turut adalah (−3,0) dan (0, −1). Persegi panjang $ABCD$ dengan titik $C$ dan $D$ terletak di dua kuadran berbeda memiliki luas daerah 20 satuan luas. Jika persegi panjang $ABCD$ dicerminkan terhadap sumbu−$x$, maka hasil pencerminan salah satu sisinya akan memotong sumbu−$x$ di titik $(m, 0)$ dan hasil pencerminan salah satu sisinya yang lain akan memotong sumbu−$y$ di titik $(0, n)$. Nilai dari $3(m + n)$ yang mungkin adalah …A. -16B. -15C. 1D. 18
- Suatu keluarga memiliki lima anak dengan anak sulung bernama Andy. Ayah memberi uang saku bulanan kepada kelima anaknya tersebut dengan ketentuan berikut. Uang saku Andy adalah dua kali lipat uang saku anak kedua, tiga kali lipat uang saku anak ketiga, empat kali lipat uang saku anak keempat, serta lima kali lipat uang saku anak kelima. Besaran uang saku anak-anak tersebut adalah bilangan bulat kelipatan ribuan rupiah. Bendy dan Cindy adalah adik dari Andy. Bendy mengeluh bahwa uang saku yang diterima adalah Rp20.000 lebih sedikit dibanding Cindy. Besaran terkecil uang saku Andy yang mungkin adalah …A. Rp60.000B. Rp80.000C. Rp120.000D. Rp240.000
- Jika $(x, y)$ adalah pasangan bilangan bulat positif yang memenuhi persamaan $$x^{2021} + y^{2} = 4y − 3,$$ Maka banyak pasangan $(x, y)$ yang memenuhi persamaan tersebut adalah …A. 3B. 2C. 1D. 0
- Misalkan B menyatakan barisan bilangan bulat yang suku-sukunya $b_{1}, b_{2}, b_{3}, b_{4}, …$ dan $f(B)$ menyatakan barisan bilangan bulat yang suku-sukunya $b_{1} − b_{2}, b_{2} − b_{3}, b_{3} − b_{4}, …$Jika semua suku dari barisan $f(f(B))$ adalah bilangan bulat $c$, dengan $c = 3$, dan diketahui $b_{21} × b_{42} = b_{21} + b_{42} = 0$, maka nilai dari $b_{2} adalah …A. 90B. 760C. 1140D. 1230
- Diketahui $n$ adalah bilangan tiga digit yang jika dibagi 7 dan 9 masing-masing memberikan sisa 1 dan 2. Jumlah nilai maksimum dan minimum dari $n$ adalah …A. 974B. 1003C. 1129D. 1130
- Berikut adalah data penjualan dari lima perusahaan A, B, C, D, dan E dalam lima tahun (2010 hingga 2014). Data diberikan dalam persentase terhadap total penjualan A. B, C, D, dan E, serta hanya tiga perusahaan teratas yang disebutkan untuk setiap tahun yang ditentukan.
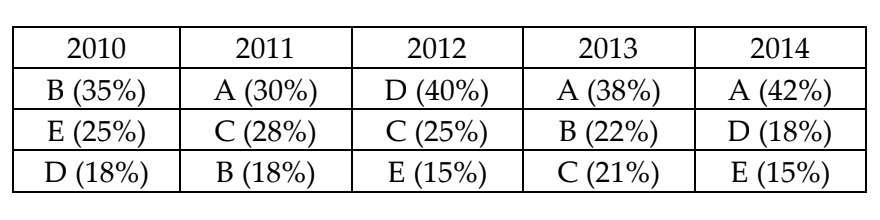Diketahui bahwa tidak ada perusahaan yang memiliki persentase yang sama dalam satu tahun dan setidaknya persentase masing-masing perusahaan 1% dari total penjualan kelima perusahaan di tahun tersebut.Jika total penjualan kelima perusahaan adalah sama setiap tahunnya, banyaknya perusahaan yang penjualannya pasti lebih besar dari perusahaan E selama lima tahun adalah …A. 1B. 2C. 3D. 4 Diagram tersebut mempresentasikan hasil survei penghasilan dan instrument investasi pilihan 1000 orang di suatu wilayah. Jika dari 1000 orang tersebut dipilih 1 orang secara acak untuk diwawancarai dan diketahui bahwa orang tersebut memiliki penghasilan kurang dari Rp4.000.000, maka peluang orang tersebut lebih memilih instrumen investasi reksadana adalah … %.
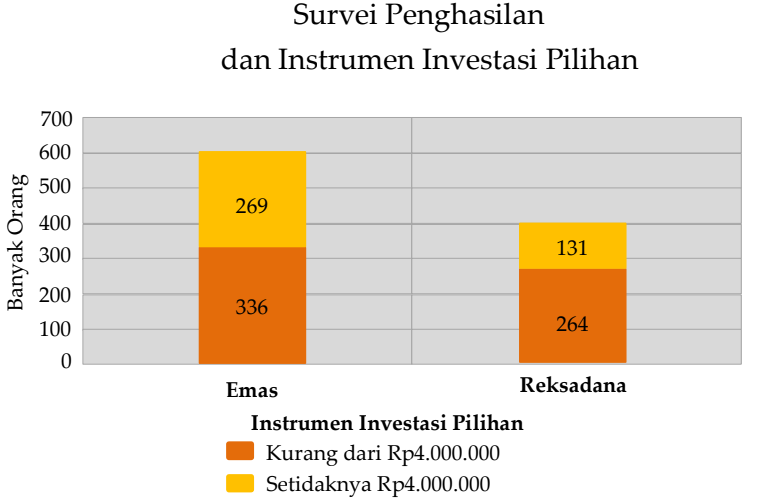A. 26B. 40C. 44D. 67Diberikan persegi panjang $ABCD$ dengan $AB = 12$ dan $BC = 6$. Titik $E, F, G, H$ dipilih sehingga $BE = BF = DG = DH = p$. Jika ruas garis $FH$ dan $EG$ berpotongan di tengah-tengah persegi panjang, dan luas daerah yang diarsir adalah 12,5% dari luas ABCD, makan nilai p adalah …
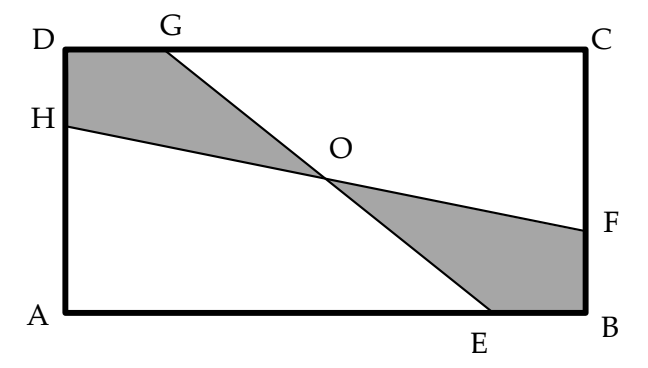A. 1/3B. 1/2C. 1D. 3/2Bintang menuliskan angka 1, 2, 3, 4, 5, 6, 7, dan 8 di baris pertaman table berikut.
Bintang ingin melakukan hal yang serupa pada baris kedua dengan suatu urutan tertentu. Setiap bilangan pada baris ketiga adalah jumlah dua bilangan di atasnya.
Banyaknya cara Bintang mengisi baris kedua sehingga semua bilangan pada baris ketiga merupakan bilangan genap adalah …A. 8B. 16C. 48D. 576
Keranjang Belanja