OSK SMP 2020

  1. Jika $a, b, c, d$ adalah bilangan bulat positif berbeda sehingga $abcd = 2020$, maka nilai terkecil yang mungkin dari $\frac{a+b}{c+d}$ adalah …
    A. $\frac{3}{507}$
    B. $\frac{5}{106}$
    C. $\frac{1}{17}$
    D. $\frac{1}{69}$
  2. Manakah di antara bilangan berikut yang merupakan bilangan prima?
    A. 2017
    B. 2019
    C. 2021
    D. 2023
  3. Jika $\Delta (a,b,c) = ab+bc+ac$, dan misalkan $x_{1}$ dan $x_{2}$ adalah bilangan yang memenuhi $\frac{1}{3} \Delta (x+1, x-2,5)=(x-2)(x+2)$, maka nilai terbesar yang mungkin dari $2x_{1}-3x_{2}$ adalah …
    A. -16
    B. 13
    C. 8
    D. $\frac{23}{2}$
  4. Jumlah $n$ suku pertama suatu deret aritmetika adalah 450. Jika suku pertama adalah $n$ dan suku ke-$n$ adalah 3, maka selisih barisan tersebut adalah …
    A. $\frac{13}{7}$
    B. $\frac{15}{7}$
    C. $\frac{13}{11}$
    D. $\frac{15}{11}$
  5. Jika $f(x)=5x-3$, maka jumlah semua $x$ yang memenuhi $(f(x))^{2}-6f(x)=-9$ adalah …
    A. 0
    B. 3
    C. $\frac{3}{5}$
    D. $\frac{6}{5}$
  6. $R_{t}$ dan $R_{k}$ berturut-turut menyatakan jari-jari tabung dan jari-jari kerucut. Jika tinggi tabung dan tinggi kerucut adalah 3600 cm, volume tabung $490\pi$ liter dan volume kerucut $30\pi$ liter, maka hubungan antara $R_{t}$ dan $R_{k}$ adalah …
    A. $7R_{t}=3R_{k}$
    B. $3R_{t}=7R_{k}$
    C. $6R_{t}=7R_{k}$
    D. $6R_{t}=3R_{k}$

  7. Perhatikan bangun setengah lingkaran berikut. Jika $CA=6$ cm dan $ED+DF=8$ cm, maka keliling bangun yang diarsir adalah …

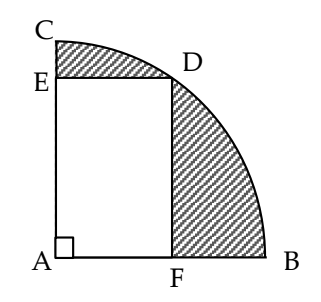    A. $\pi +36$
    B. $6\pi +12$
    C. $3\pi +36$
    D. $3\pi +12$
  8. Di dalam sebuah kerucut terdapat sebuah balok. Volume kerucut $600\pi$ $cm^{3}$ dan jari-jarinya 10 cm. Jika tinggi balok setengah tinggi kerucut, maka volume balok terbesar yang ada di dalam kerucut tersebut adalah …
    A. $72 cm^{3}$
    B. $225 cm^{3}$
    C. $450 cm^{3}$
    D. $900 cm^{3}$
  9. Pada suatu pameran seni di sekolah, akan dipajang 8 lukisan istimewa terdiri dari 3 lukisan cat air dan 5 lukisan cat minyak. Semua lukisan tersebut saling berbeda. Untuk alasan artistic, maka setiap lukisan cat air akan diletakkan di antara dua lukisan cat minyak. Banyak kemungkinan susunan lukisan tersebut adalah …
    A. 0
    B. 24
    C. 27
    D. 54
  10. Sebuah dadu berisi enam dilempar sebanyak $n$ kali, $n > 0$. Jika rata-rata mata dadu yang keluar adalah $\frac{1}{4}n$, maka median dari seluruh nilai $n$ yang mungkin adalah …
    A. 11
    B. 12
    C. 13
    D. 14
  11. Jika $2^{5n}$ dan $5^{2m}$ adalah faktor dari $2020^{2020}$, maka jumlah digit dari nilai maksimum $m+2n$ adalah …
    A. 16
    B. 18
    C. 20
    D. 22
  12. Diberikan empat bilangan bulat positif a, b, c dan d yang memenuhi pertaksamaan $a<b<c<d$. Diketahui pula $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d}=1$. Banyaknya pasangan bilangan $(a,b,c,d)$ yang memenuhi permasalahan di atas adalah …
    A. 1
    B. 4
    C. 6
    D. 9
  13. Perhatikan barisan bilangan berikut.
    1, 2, 4, 8, 15, 26, ?, ?, ?, …
    Tiga bilangan selanjutnya berturut-turut adalah …
    A. 37,49,71
    B. 37,61,99
    C. 42,58,74
    D. 42,64,93
  14. Jika $x_{1}$ dan $x_{2}$ dengan $x_{1} < x_{2}$ adalah solusi yang memenuhi persamaan $x^{(x^{x})}=(x^{x})^{x}$, maka $25x_{1} \text{ }^{2}+4x_{2}\text{ }^{2}-10x_{1}x_{2}$ adalah …
    A. 1
    B. 4
    C. 64
    D. 19
  15. Diketahui tiga bilangan terurut $(x,y,z)$ dengan $x,y$ dan $z$ adalah bilangan bulat positif yang memenuhi $(3x+y-1)^{y+z}=729$. Jika himpunan selesainnya adalah ${(x_{1},y_{1},z_{1}),(x_{2},y_{2},z_{2}),…,(x_{n},y_{n},z_{n})}$, maka nilai dari $x_{1}+x_{2}+…+x_{n}+y_{1}+y_{2}+…+y{n}+z_{1}+z_{2}+…+z_{n}$ adalah …
    A. 17
    B. 18
    C. 24
    D. 29

  16. Perhatikan gambar $\Delta ABC$ berikut.

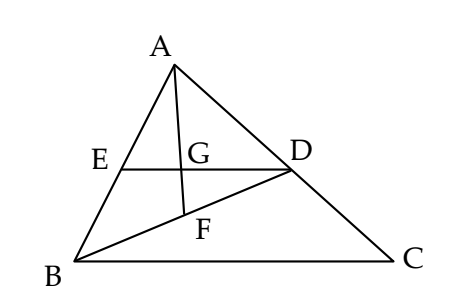    Diketahui $D$ titik tengah sisi $AC, F$ titik tengah sisi $BD$ dan $DE$ sejajar $BC$. Jika $G$ adalah titik potong $AF$ dan $DE$, maka perbandingan $BC : DG$ adalah …
    A. 12 : 1
    B. 8 : 1
    C. 6 : 1
    D. 4 : 1
  17. Diketahui suatu bilangan terdiri dari 6 digit. Jika digit terakhirnya sama dengan digit pertama, maka banyak kemungkinan bilangan tersebut adalah …
    A. 90000
    B. 100000
    C. 900000
    D. 1000000
  18. Siswa-siswi sebuah SMP yang menyaksikan pertandingan sepak bola, oleh panitia diberi Nomor Undian Doorprize (NUD) pada kertas yang terdiri dari atas empat digit. Panitia pertandingan sudah menyiapkan hadiah untuk semua NUD untung, yaitu nomor yang digit ke-empatnya merupakan pengurangan bilangan dua digit pertama oleh bilangan digit ketiga. Contohnya 1155 $\to$ 11 – 5 = 6 adalah NUD untung. Banyak hadiah yang harus disediakan oleh panitia adalah …
    A. 42
    B. 44
    C. 45
    D. 46
  19. A adalah himpunan semua bilangan tiga digit yang tidak memuat 0 dan semua digitnya berbeda. Jika x,y,z berturut-turut adalah rata-rata, median dan jangkauan dari semua anggota A, maka nilai dari $x-y+z$ adalah …
    A. 445
    B. 504
    C. 555
    D. 864
  20. Bilangan $\frac{b}{a}$ terbesar dengan $a,b$ positif sedemikian sehingga $\frac{5}{a}+20b$ merupakan bilangan kuadrat sempurna yang kurang dari 2020 adalah …
    A. 2800
    B. 5500
    C. 6400
    D. 7500
  21. Jika $a,b$ bilangan real positif dengan $a^{505}+b^{505}=1$, maka nilai minimum dari $a^{2020}+b^{2020}$ adalah …
    A. 1
    B. $\frac{1}{2}$
    C. $\frac{1}{4}$
    D. $\frac{1}{8}$
  22. Diketahui segi delapan $ABCDEFGH$ dengan panjang sisinya 2 cm. Akan dipilih secara acak 3 titik sudutnya dan digunakan untuk membentuk suatu segitiga yang akan dihitung luas daerahnya. Jika A adalah himpunan semua luas daerah segitiga yang mungkin dan jumlah semua anggota A adalah $(a+b\sqrt{2})cm^{2}$, maka nilai dari $a+b$ adalah …
    A. 9
    B. 12
    C. 21
    D. 33
  23. Diketahui persegipanjang ABCD dibidang koordinat kartesius dengan A dan B di sumbu X, D di sumbu Y dan C di kuadran 1. Ada 4 jenis rotasi yang akan dilakukan terhadap persegi panjang ABCD: $1.R(C, -90\circ), 2.R(A, 90\circ), 3.R(C, 90\circ), 4.R(A, -90\circ)$ dimana $R(C, 90\circ)$ berarti rotasi $90\circ$ berlawanan arah jarum jam dengan pusat C. Jika ABCD dirotasi berturut-turut dengan urutan 1, 2, 3, 4, 1, 2, 3, 4, 1, 2, 3, 4, 1, 2, 3, 4, 1, 2, 3 dan diperoleh koordinat akhir A adalah (38, 47), maka keliling persegi panjang ABCD adalah … satuan panjang.
    A. 9
    B. 17
    C. 38
    D. 47
  24. Pada suatu kotak terdapat 40 bola warna merah dan hijau. Dua buah bola diambil secara acak dan diamati warnanya. Jika peluang bahwa terambil kedua bola berwarna merah adalah $\frac{5}{12}$ , maka banyaknya bola merah di dalam kotak semula adalah … buah.
    A. 20
    B. 22
    C. 25
    D. 26
  25. Suatu kelas terdiri dari 35 siswa. Pada saat ulangan matematika terdapat 2 orang siswa berhalangan, misalnya siswa A dan B. Nilai ulangan pada awalnya dicatat hanya dari 33 siswa dan memiliki rata-rata 80. Setelah ditambah nilai susulan dua siswa yang berhalangan tersebut, nilai rata-rata kelas menjadi 78. Jika nilai A dua kali lipat lebih tinggi dibandingkan nilai B, maka selisih nilai A dan B adalah …
    A. 15
    B. 20
    C. 30
    D. 55
Keranjang Belanja
Scroll to Top