OSK SMP 2017

  1. Misalkan $n$ adalah suatu bilangan bulat positif. Jumlah tiga bilangan prima $3n-4, 4n-5$ dan $5n-3$ adalah …
    A. 12
    B. 14
    C. 15
    D. 17
  2. Diketahui $a$ dan $b$ adalah dua bilangan bulat positif, serta $b$ merupakan bilangan ganjil yang lebih kecil dari 2017. Jika $\frac{1}{a}+\frac{4}{b}=\frac{1}{12}$, maka pasangan bilangan $(a,b)$ yang mungkin ada sebanyak …
    A. 2
    B. 3
    C. 5
    D. 8

  3. Grafik berikut mengilustrasikan lomba lari 100 m yang diikuti oleh tiga orang siswa A, B dan C. Berdasarkan grafik tersebut, pernyataan yang benar adalah …

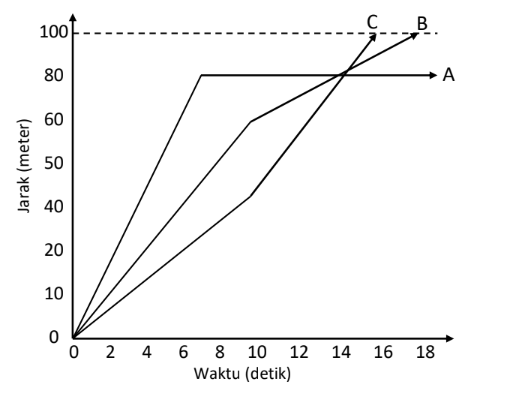    A. Pelari C selalu berlari paling depan
    B. Pelari B disusul oleh C sebelum garis finis
    C. Pelari A paling cepat berlari sampai ke garis finis
    D. Pelari B memenangi lomba karena berlari dengan kecepatan konstan
  4. Jika bilangan bulat positif $x$ dan $y$ merupakan solusi system persamaan linier
    $x+2y=p+6$
    $2x-y=25-2p$
    maka banyak nilai $p$ adalah …
    A. 2
    B. 3
    C. 4
    D. 5
  5. Diketahui fungsi $f$ memenuhi persamaan $5f\left( \frac{1}{x} \right)+\frac{f(2x)}{x^{2}}=x$ untuk $x \neq 0$. Nilai $f(1)$ sama dengan …
    A. $\frac{3}{7}$
    B. $\frac{3}{14}$
    C. $\frac{3}{18}$
    D. $\frac{1}{7}$
  6. Pada jajar genjang ABCD, jarak antara sepasang sisi sejajar pertama adalah 4 cm dan jarak antara sepasang sisi sejajar lainnya adalah 9 cm. Luas jajar genjang ABCD adalah …

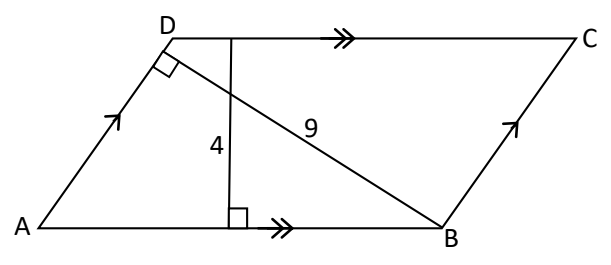    A. minimal 36 $cm^{2}$
    B. tepat 36 $cm^{2}$
    C. maksimal 36 $cm^{2}$
    D. antara 36 $cm^{2}$ dan 81 $cm^{2}$

  7. Lingkaran pada gambar berikut mempunyai radius 1 satuan panjang dan $\angle DAB=30\circ$. Luas daerah trapesium $ABCD$ yang diarsir adalah …

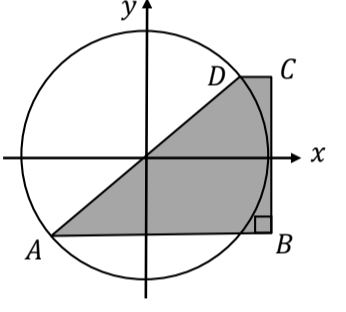    A. $\frac{1}{2}$
    B. 1
    C. $\frac{1}{2}\sqrt{3}$
    D. $\frac{1}{2}+\frac{1}{2}\sqrt{3}$

  8. Diketahui persegi panjang $ABCD$ dengan $AB=12$ dan $BC=5$. Panjang lintasan $DPQB$ pada gambar berikut adalah …

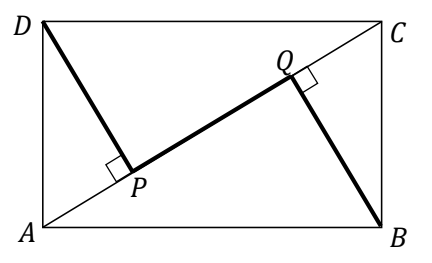    A. $\frac{119}{13}$
    B. $\frac{120}{13}$
    C. $\frac{214}{13}$
    D. $\frac{239}{13}$
  9. Diketahui $M=\{10,11,12,…,99\}$ dan $A$ adalah himpunan bagian dari $M$ yang mempunyai 4 anggota. Jika jumlah semua anggota $A$ merupakan suatu bilangan genap, maka banyak himpunan $A$ yang mungkin adalah …
    A. 1 980
    B. 148 995
    C. 297 990
    D. 299 970
  10. Data 4 pengamatan berupa bilangan positif yang sudah diurutkan dilambangkan dengan $x_{1},x_{2},x_{3}$ dan $x_{4}$. Jika jangkauan data tersebut adalah 16, $x_{1}=\frac{1}{6}$median, $x_{2}=\frac{1}{2}$median, dan $x_{3}=x_{4}$, maka rata-rata data tersebut adalah …
    A. 10
    B. 11
    C. 12
    D. 13
 
ISIAN SINGKAT
  1. Diketahui $n$ dan $k$ adalah dua bilangan bulat. Jika terdapat tepat satu nilai $k$ yang memenuhi pertidaksamaan $\frac{8}{15}<\frac{n}{n+k}<\frac{7}{13}$, maka nilai $n$ terbesar yang mungkin adalah …
  2. Nilai $1 + 2.2 + 3.2^{2} + 4.2^{3} + … + 2018.2^{2017}$ sama dengan …
  3. Diketahui $p,q,r,s$ adalah bilangan-bilangan tidak nol. Bilangan $r$ dan $s$ adalah solusi persamaan $x^{2}+px+q=0$ serta $p$ dan $q$ adalah solusi persamaan $x^{2}+rx+s=0$. Nilai $p+q+r+s$ sama dengan …
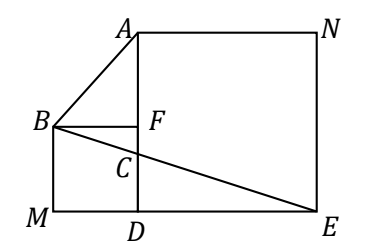
  4. Misalkan $ADEN$ dan $BMDF$ adalah persegi dengan $F$ merupakan titik tengah $AD$. Luas segitiga $CDE$ adalah 6 satuan luas. Luas segitiga $ABC$ adalah …
  5. Tersedia 10 loket pelayanan pelanggan pada sebuah bank. Terdapat sejumlah pelanggan yang sedang berada dalam satu baris antrian. Peluang bahwa 4 orang pertama pada antrian dilayani di loket berbeda, dan orang ke-5 pada antrian dilayani di loket yang sama dengan salah satu dari 4 orang sebelumnya adalah …
Keranjang Belanja
Scroll to Top