OSK SMP 2011

  1. Nilai $\frac{1}{8!}-\frac{2}{9!}+\frac{3}{10!}$ = …
    A. 113/10!
    B. 91/10!
    C. 73/10!
    D. 71/10!
    E. 4/10!
  2. Menggunakan angka-angka 1,2,5,6 dan 9 akan dibentuk bilangan genap yang terdiri dari lima angka. Jika tidak ada angka yang berulang, maka selisih bilangan terbesar dan terkecil adalah …
    A. 70820
    B. 79524
    C. 80952
    D. 81236
    E. 83916

  3. Pada gambar berikut tabung berisi air, tinggi dan diameter tabung tersebut adalah 18 cm dan 6 cm.

    Kemudian ke dalam tabung dimasukkan 3 bola pejal yang identik (sama bentuk) sehingga bola tersebut menyinggung sisi tabung dan air dalam tabung keluar, maka sisa air di dalam tabung adalah … $cm^{3}$.

    A. $51\pi$
    B. $52\pi$
    C. $53\pi$
    D. $54\pi$
    E. $55\pi$

  4. Seorang ilmuwan melakukan percobaan terhadap 50 ekor kelinci, dan melaporkan hasilnya sebagai berikut:

    • 25 ekor diantarannya kelinci jantan.
    • 25 ekor di laatih menghindari jebakan, 10 ekor diantarannya jantan.
    • 20 ekor (dari total 50 ekor) berhasil menghindari jebakan, 4 ekor diantarannya jantan.
    • 15 ekor yang pernah dilatih berhasil menghindari jebakan, 3 ekor diantarannya jantan.
    Berapa ekor kelinci betina yang tidak pernah dilatih, tidak dapat menghindari jebakan?
    A. 5
    B. 6
    C. 7
    D. 8
    E. 9
  5. Banyaknya bilangan bulat $x$ sehingga $\frac{1}{2+\sqrt{x}}+\frac{1}{2-\sqrt{x}}$ merupakan bilangan bulat adalah …
    A. 2
    B. 3
    C. 5
    D. 6
    E. 7
  6. Urutan tiga bilangan $2^{4444},3^{3333}$ dan $4^{2222}$ dari yang terkecil sampai yang terbesar adalah:
    A. $2^{4444},4^{2222},3^{3333}$
    B. $2^{4444},3^{3333},4^{2222}$
    C. $3^{3333},4^{2222},2^{4444}$
    D. $4^{2222},3^{3333},2^{4444}$
    E. $3^{3333},2^{4444},4^{2222}$
  7. Lima pasang suami istri akan duduk di 10 kursi secara memanjang. Banyaknya cara mengatur tempat duduk mereka sehingga setiap pasang suami istri duduk berdampingan adalah …
    A. 3800
    B. 3820
    C. 3840
    D. 3900
    E. 3940
  8. Dalam sebuah kotak berisi 15 telur, 5 telur diantaranya rusak. Untuk memisahkan telur baik dan telur yang rusak dilakukan pengetesan satu persatu tanpa pengembalian. Peluang diperoleh telur rusak ke 3 pada pengetesan ke 5 adalah …
    A. $\frac{80}{1001}$
    B. $\frac{90}{1001}$
    C. $\frac{100}{1001}$
    D. $\frac{110}{1001}$
    E. $\frac{120}{1001}$
  9. Diketahui limas beraturan $T.ABCD$, panjang rusuk $AB$ 2 cm dan $TA$ 4 cm. Jarak titik $B$ dan rusuk $TD$ adalah …
    A. $\sqrt{5}$
    B. $\sqrt{6}$
    C. $\sqrt{7}$
    D. $2\sqrt{5}$
    E. $2\sqrt{6}$

  10. Sembilan lingkaran kongruen terletak didalam persegi seperti terlihat pada gambar. Jika keliling sebuah lingkaran 62,8 cm dengan $\pi$ = 3,14, maka luas daerah yang diarsir adalah …$cm^{2}$.

    A. 344
    B. 364
    C. 484
    D. 688
    E. 728
  11. Suatu jam dinding selalu menghasilkan keterlambatan lima menit untuk setiap jam nya. Jika saat sekarang jam tersebut menunjukkan waktu yang tepat, maka jam tersebut akan menunjukkan waktu yang tepat setelah … jam.
    A. 105
    B. 110
    C. 114
    D. 124
    E. 144
  12. Didalam kotak terdapat 18 bola identik (berbentuk sama), 5 berwarna hitam, 6 berwarna putih dan 7 berwarna hijau. Jika diambil dua bola secara acak, maka peluang yang terambil bola berwarna sama adalah …
    A. $\frac{46}{153}$
    B. $\frac{13}{36}$
    C. $\frac{4}{105}$
    D. $\frac{55}{162}$
    E. $\frac{55}{152}$

  13. Perhatikan gambar di atas, persegi $ABCD$ dengan panjang sisi 14 cm menyinggung lingkaran. Masing-masing sisi persegi di buat setengah lingkaran dengan diameter sisi persegi tersebut. Jika $\pi=3,14$, maka luas daerah yang di arsir adalah … $cm^2$.

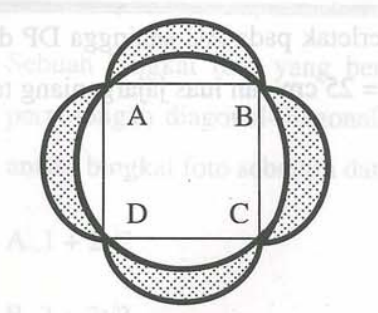    A. 49
    B. 56
    C. 112
    D. 178
    E. 196
  14. Diketahui $2^{2x}+2^{-2x}=2$. Nilai $2^{x}+2^{-x}$ = …
    A. 1
    B. 2
    C. $\sqrt{2}$
    D. 3
    E. $\sqrt{3}$
  15. Rataan usia kelompok guru dan profesor adalah 40 tahun. Jika rataan kelompok guru adalah 35 tahun sedangkan rataan kelompok profesor adalah 50 tahun, perbandingan banyaknya guru dengan profesor adalah …
    A. 2:1
    B. 1:2
    C. 3:2
    D. 2:3
    E. 3:4
  16. Diketahui jajargenjang $ABCD$. Titik $P$ dan $Q$ terletak pada $AC$ sehingga $DP$ dan $BQ$ tegak lurus $AC$. Jika panjang $AD = 13$ cm, $AC = 25$ cm dan luas jajargenjang tersebut adalah $125 cm^{2}$, maka panjang $PQ$ adalah … cm.
    A. 1/2
    B. 1
    C. $\sqrt{2}$
    D. $\sqrt{3}$
    E. 43
  17. $\sqrt{54+14\sqrt{5}}+\sqrt{12-2\sqrt{35}}+\sqrt{32-10\sqrt{7}}$ = …
    A. 10
    B. 11
    C. 12
    D. $5\sqrt{6}$
    E. $6\sqrt{6}$
  18. Hasil penjumlahan $1! + 2! + 3! + … + 2011!$ adalah suatu bilangan yang angka satuannya adalah …
    A. 3
    B. 4
    C. 5
    D. $\sqrt{6}$
    E. $\sqrt{7}$
  19. Lima orang akan pergi ke pantai menggunakan sebuah mobil berkapasitas 6 tempat duduk. Jika hanya ada dua orang yang bisa menjadi sopir, maka banyaknya cara mengatur tempat duduk mereka di dalam mobil adalah …
    A. 60
    B. 120
    C. 180
    D. 240
    E. 280
  20. Sebuah bingkai foto yang berbentuk persegi di putar $45\circ$ dengan sumbu putar titik perpotongan diagonal-diagonalnya. Jika panjang sisi persegi adalah 1 cm, luas irisan antara bingkai foto sebelum dan sesudah diputar adalah … $cm^{2}$.
    A. $1+2\sqrt{2}$
    B. $2+2\sqrt{2}$
    C. 1
    D. $2-2\sqrt{2}$
    E. $2\sqrt{2}-2$
 
ISIAN SINGKAT
  1. Lima permen identik (berbentuk sama), satu rasa apel, dua rasa jeruk dan dua rasa jahe akan dibagikan kepada lima sekawan Anto, Bono, Carli, Dede dan Edo, sehingga masing-masing mendapat satu permen. Peluang Anto mendapat permen rasa jahe adalah …
  2. Jumlah angka-angka dari hasil kali bilangan 999999999 dengan 123456789 adalah …
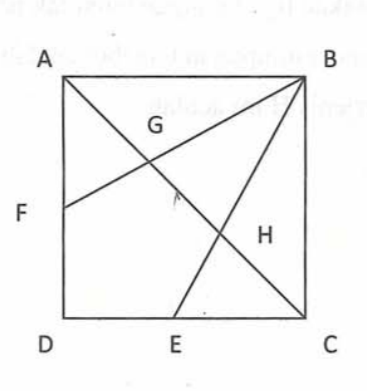
  3. Perhatikan gambar berikut. $ABCD$ persegi dengan panjang sisi-sisinya adalah 2 cm. E adalah titik tengah $CD$ dan $F$ adalah titik tengah $AD$. Luas daerah $EDFGH$ adalah … $cm^{2}$.
  4. Nilai jumlahan bilangan berikut adalah … $$1^{2}-2^{2}+3^{2}-4^{2}+5^{2}-…-2010^{2}+2011^{2}$$
  5. Jika barisan $x_{1},x_{2},x_{3}, …$ memenuhi $x_{1}+x_{2}+…+x_{n}=n^{3}$ untuk semua $n$ bilangan asli, maka $x_{100}$ = …
  6. Semua pasangan bilangan bulat $(a,b)$ yang memenuhi $2^{a}=b^{2}-1$ adalah …
  7. Tersedia beberapa angka 2,0 dan 1. Angka dua ada sebanyak lima buah masing-masing berwarna merah, hijau, kuning, biru dan nila. Angka nol dan satu masing-masing ada sebanyak empat buah dengan warna masing-masing merah, hijau, kuning dan biru. Selanjutnya menggunakan angka-angka tersebut akan dibentuk bilangan 2011 sehingga angka-angka yang bersebelahan tidak boleh sewarna. Contoh pewarnaan yang dimaksud: 2(merah) 0(hijau) 1(merah) 1(biru). Contoh bukan pewarnaan yang dimaksud: 2(merah) 0(hijau) 1(hijau) 1(biru). Banyaknya bilangan 2011 dengan komposisi pewarnaan tersebut adalah …
  8. Sebuah kotak berisi 500 kelereng berukuran sama yang terdiri dari 5 warna dimana masing-masing kelereng sewarna berjumlah 100. Minimum banyaknya kelereng yang harus diambil secara acak sedemikian sehingga kelereng yang terambil di jamin memuat sedikitnya 5 kelereng yang berwarna sama adalah …
  9. Jika $(3+4)(3^{2}+4^{2})(3^{4}+4^{4})(3^{8}+4^{8})(3^{16}+4^{16})(3^{32}+4^{32})=(4^{x}-3^{y})$, maka $x-y$ = …
  10. Suatu himpunan disebut berjenis $H$ jika memenuhi sifat:
    a. Himpunan tersebut beranggotakan tiga bilangan bulat tak negatif.
    b. Rata-rata ketiga bilangan anggota himpunan tersebut adalah 15.
    Banyaknya semua himpunan berjenis $H$ ini adalah …
Keranjang Belanja
Scroll to Top