- Misalkan $p$ dan $q$ adalah bilangan asli yang memenuhi persamaan $$p(p − 70) + q(q − 70) + 2pq = 2024.$$ Banyaknya pasangan (p, q) yang mungkin adalah …
- Misalkan $n$ adalah bilangan bulat positif tiga digit. Didefinisikan $f(n)$ adalah jumlah $n$ dan semua digit dari $n$. Sebagai contoh, $f(231) = 231 + 2 + 3 + 1 =237$. Jika $a$ dan $b$ juga bilangan tiga digit sehingga $f(a) = 204$ dan $f(b) = 535$, maka nilai terkecil yang mungkin dari $a + b$ adalah …
- Bilangan kaset adalah bilangan bulat positif yang seluruh digitnya prima dan hasil perkalian seluruh digitnya sama dengan 10 kali hasil penjumlahan seluruh digitnya. Banyaknya bilangan kaset adalah …
- Banyaknya bilangan bulat positif yang kurang dari 101 dan bisa dinyatakan sebagai hasil penjumlahan setidaknya 4 bilangan bulat positif berurutan adalah …
- Diketahui persamaan $$\frac{1}{x − y − z}=\frac{1}{y}+\frac{1}{z}$$ Banyaknya triple $(x, y, z)$ yang memenuhi persamaan di atas dimana $x, y$ dan $z$ bilangan prima atau negatif bilangan prima adalah …
- Diberikan dua fungsi $$f(x) = x^3 − px^2 + 189x − q$$ $$g(x) = x^3 − rx^2 + 144x − s.$$ Akar $f(x)$ adalah $a, a$ dan $b$, sedangkan akar $g(x)$ adalah $a, b$ dan $b$. Jika $a, b, p, q, r$ dan $s$ bilangan bulat positif, maka nilai $(p + q) − (r + s)$ = …
- Misalkan $$k = \frac{pq + 2024}{p + 2024} + \frac{qr + 2024}{(q + 1) 2024} +\frac{rs + 2024}{r + 2024} +\frac{sp + 2024}{(s + 1) 2024}$$ dengan $p, q, r, s$ bilangan real positif dan $pqrs = 2024^2$. Jika $x$ adalah nilai minimum dari $k$, maka nilai dari $1000x$ adalah …
- Pada fungsi $f(x)$ berlaku persamaan $(x − 1) ∙ f(x + 1) = (x + 2) ∙ f(x)$ Jika $\frac{f(2024)}{f(2)}= a$, maka banyaknya faktor prima $a$ adalah …
- Diketahui untuk setiap nilai $a$ dan $b$ pada fungsi $f$ dan $g$ memenuhi persamaan-persamaan berikut: $$2f(a) + 3g(b) = 6$$ $$3f(b) + 2g(a) = 7$$ $$[f(a)]^2 + [g(a)]^2 = 1$$ $$f(a + b) = f(a) g(b) + f(b)g(a).$$ Nilai dari $f(a + b)$ = …
- Suatu fungsi kuadrat $y = f(x)$ melalui titik $(0,3)$ dan memenuhi $−1 \le f(−2) \le 1$ dan $−2 \le f(2) \le 2$. Jika nilai maksimum fungsi kuadrat $y = f(x)$ adalah $M$, maka nilai $840M$ = …
- Perhatikan gambar dibawah ini.
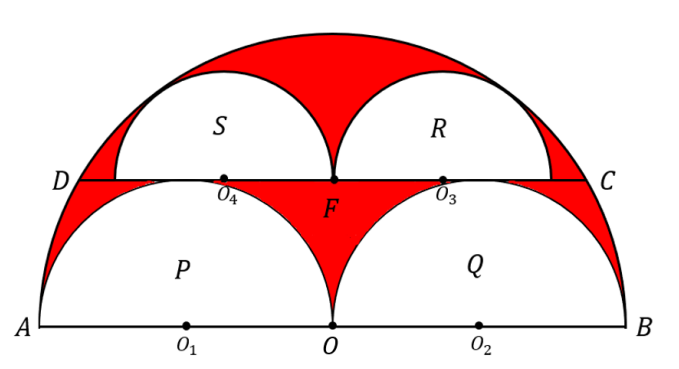
Setengah lingkaran $X$ memiliki pusat $O$ dan diameter $AB$. Di dalam setengah lingkaran $X$ terdapat 4 buah setengah lingkaran $P, Q, R$ dan $S$ dengan masing-masing pusatnya $O_1,O_2,O_3$ dan $O_4$ . Garis $AO$ dan $OB$ merupakan diameter setengah lingkaran $P$ dan $Q$. Garis $CD$ adalah tali busur setengah lingkaran $X$ yang sejajar dengan garis $AB$ dan menyinggung setengah lingkaran $P$ dan $Q$. Titik $F$ adalah titik tengah $CD$. Diameter setengah lingkaran $R$ dan $S$ berada pada garis $CD$ sehingga kedua setengah lingkaran tersebut bersinggungan di titik $F$ dan menyinggung busur setengah lingkaran $X$. Jika perbandingan luas daerah yang berwarna merah dan luas daerah yang berwarna putih dapat dinyatakan dalam bentuk perbandingan yang paling sederhana $A:B$, maka nilai dari $A + B$ adalah … - Diketahui persegi $ABCD$ dengan panjang sisi 4 satuan panjang. Titik $D$ diputar 600 searah jarum jam dengan pusat putaran titik $A$ dan diperoleh titik $D′$. Titik $A, B$ dan $C$ masing-masing dicerminkan terhadap titik $D’$ dan diperoleh masing-masing titik $A′,B′$ dan $C′$.
Jika luas segiempat A′B′C′D′ sama dengan $a − b\sqrt{3}$ satuan luas, maka nilai $a \text{ x } b$ = …
- Perhatikan segitiga siku-siku $ABC$ berikut.
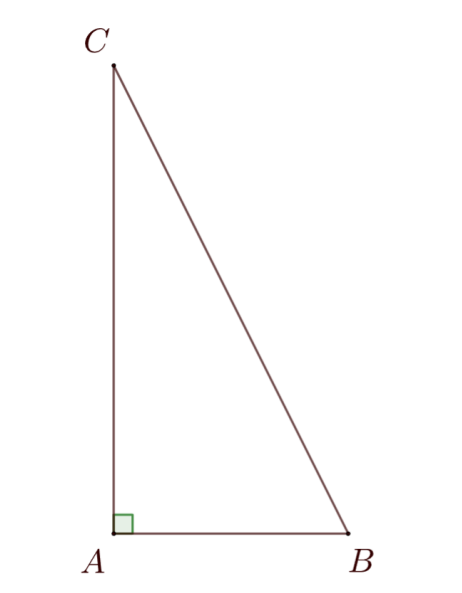
Diketahui lingkaran $L$ yang jari-jarinya $r$ cm dengan $r$ bilangan bulat, menyinggung ketiga sisi segitiga $ABC$. Kemudian, digambar garis $\mathscr{l}$ yang melalui titik pusat lingkaran $L$ dan sejajar $BC$. Garis $\mathscr{l}$ memotong $AB$ di $P$ dan $AC$ di $Q$, serta memotong lingkaran $L$ di $X$ dan $Y$. Jarak $X$ ke $AB$ kurang dari jarak $Y$ ke $AB$. Jika $PX$ = 1,5 cm dan $QY$ = 4 cm, maka luas daerah lingkaran $L$ adalah …$\pi$ cm2. - Sebuah perusahaan akan mengepak bola-bola dengan ukuran diameter 10 cm ke dalam suatu wadah berbentuk balok dengan ukuran bagian dalam 50 cm × 50 cm × 60 cm. Maksimum banyaknya bola yang dapat dimasukkan ke dalam wadah tersebut adalah …
- Segi enam $ABCDEF$ memiliki sisi yang sama panjang dan semua sudutnya kurang dari $180∘$, serta $AB$ sejajar $DE, BC$ sejajar $EF, CD$ sejajar $FA$. Koordinat $A = (0,0) , B = (x_b, 2), C = (x_c, y_c), D = (x_d, 10), E = (0, y_e), F = (x_f, y_f)$ dan sudut $\angle FAB = 120∘$. Ordinat dari semua titik sudut segi enam merupakan elemen dari $\{0,2,4,6,8,10\}$ dan tidak ada yang bernilai sama. Luas daerah $ABCDEF$ dapat ditulis dalam bentuk $q\sqrt{p}$, dengan $q$ merupakan bilangan bulat dan $p$ merupakan bilangan prima. Nilai dari $p + q$ = …
- Kelompok $A$ terdiri atas empat bilangan bulat berbeda dengan rata-rata 76 dan jangkauan 10. Kelompok $B$ terdiri atas lima data bilangan bulat berbeda dengan rata-rata 80 dan jangkauan 6. Kelompok $C$ adalah gabungan data dari kelompok $A$ dan $B$ yang berbeda. Banyaknya kemungkinan kelompok $C$ yang mempunyai rata-rata lebih besar dari rata-rata gabungan kelompok $A$ dan $B$ adalah …
- Diketahui rata-rata dari lima bilangan 6, 11, 9, 7, dan $x$ sama dengan mediannya. Jika jumlah semua nilai $x$ yang mungkin adalah $R$, maka $4R$ = …
- Diberikan himpunan $S_n = \{1,2, ⋯ , n\}$ yang beranggotakan $n$ bilangan asli pertama. Misalkan sebuah himpunan bagian akan dipilih, serta diasumsikan setiap himpunan bagian tersebut memiliki peluang yang sama untuk terpilih. Selanjutnya didefinisikan $p(n)$ sebagai peluang terpilihnya himpunan bagian yang di antara anggotanya tidak terdapat dua bilangan bulat berjumlah $n + 1$. Sebagai contoh, dari himpunan $S_4=\{1,2,3,4\}$, terdapat 16 himpunan bagian yang dapat dibentuk, yaitu $\emptyset$, {1}, {2}, {3}, {4}, {1,2}, {1,3}, {1,4}, {2,3}, {2,4}, {3,4}, {1,2,3}, {1,2,4}, {1,3,4}, {2,3,4}, {1,2,3,4}.
Terdapat 7 himpunan bagian yang di antara anggotanya adalah dua bilangan bulat berjumlah 5 (karena $n$ + 1 = 4 + 1 = 5 ), yaitu {1,4}, {2,3}, {1,2,3}, {1,2,4}, {1,3,4}, {2,3,4}, {1,2,3,4}. Perhatikan bahwa sembilan himpunan bagian lainnya tidak memiliki sifat tersebut, sehingga $p(4) =\frac{9}{16}$. Bilangan genap $n$ terkecil sehingga $p(n) < \frac{1}{4}$ adalah … - Dari sepuluh orang atlet tenis meja putra di Tim Raja Ping Pong akan dipilih empat pasangan ganda putra untuk didaftarkan mengikuti kompetisi nasional 2024. Liam dan Kadek adalah dua dari sepuluh atlet tersebut. Keduanya tidak boleh dipasangkan karena memiliki tipe permainan yang sama. Banyaknya kemungkinan empat pasangan yang didaftarkan adalah …
- Di dalam kotak terdapat 100 buah sapu tangan merah, 80 buah sapu tangan hijau, 60 buah sapu tangan biru, dan 40 buah sapu tangan hitam. Seorang anak mengambil satu buah sapu tangan pada setiap pengambilan dengan mata tertutup. banyaknya pengambilan minimum yang diperlukan untuk menjamin dia memperoleh 13 pasang sapu tangan (sepasang sapu tangan terdiri dari 2 buah sapu tangan dengan warna yang sama) adalah …
Keranjang Belanja
