A. ISIAN SINGKAT
- Simbol $\begin{vmatrix}
a & b \\
c & d
\end{vmatrix}=k$maksudnya adalah $ad − bc = k$. Jumlah semua nilai $x$ yang memenuhi$\begin{vmatrix}
x-2 & -2 \\
-x & x+4
\end{vmatrix}=2x$ adalah … - Diketahui A dan B bilangan dua digit, C bilangan tiga digit, dan A + B = C. Tujuh digit pembentuk bilangan A, B, C, yaitu 1, 2, 4, 5, 6, 7, 8 masing-masing digunakan tepat satu kali. Digit satuan dari C adalah 6. Bilangan C yang dimaksud adalah …
- Sebuah balok memiliki panjang $a$ cm, lebar $b$ cm, dan tinggi $c$ cm, di mana $a, b, c$ merupakan bilangan asli. Diketahui bahwa volume balok 240 $cm^3$ dan $a + b + c = 19$ serta $a > b > c > 3$. Luas semua sisi balok yang memiliki rusuk berukuran $b$ dan $c$ adalah … $cm^2$
- Misalkan $(x, y)$ adalah koordinat titik yang memenuhi persamaan $(4 − x)^2 + (y − 3)^2 =25$. Misalkan pula $(a, b)$ membuat $x^2 + y^2$ bernilai maksimum dan $(c, d)$ membuat $x^2 + y^2$ bernilai minimum. Nilai dari $ac + bd$ adalah …
- Jika $f(x) = x^4 + 4x^3 + 6x^2 + 4x + 10$, maka nilai dari $f(\sqrt[4]{5} − 1)$ adalah …
- Jika suatu pekerjaan dapat dikerjakan dengan mesin A, B, atau C saja, maka pekerjaan tersebut akan selesai berturut-turut dalam waktu 30 menit, 36 menit, atau 45 menit. Jika ketiga mesin tersebut digunakan bersama-sama selama 6 menit, maka bagian dari pekerjaan tersebut yang akan selesai sebesar … bagian.
- Misalkan $A = \{(x, y) | y − x \le 2, 2x + y \le 2, y \le 0\}$ dan $B = \{(x, y) | 2y − 3x \le 6, kx + 2y \le 2k, y \le 0\}$. Nilai $k$ sehingga luas daerah $B$ dua kali luas daerah $A$ adalah …
- Tiga buah persegi masing-masing panjang sisinya 6 cm, 10 cm, dan 8 cm disusun seperti gambar berikut ini.
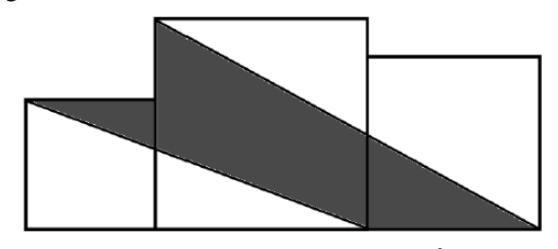
Luas daerah yang diarsir adalah … $cm^2$. - Diberikan seperempat lingkaran $PQS$ berada di dalam persegi $PQRS$, dan dua buah setengah lingkaran $PQ$ dan $PS$ di dalam $PQS$ seperti ditunjukkan pada gambar di bawah.
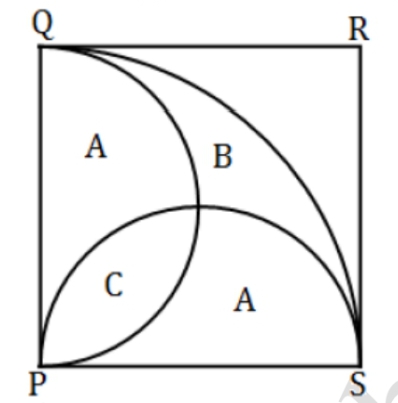
Jika persegi $PQRS$ memiliki panjang sisi $m$, maka perbandingan luas daerah $2A$ dan $B$ adalah … - Di rumah Pak Budi yang sedang ditinggal pergi berlibur, lampu teras diberi sakelar otomatis yang akan mulai menyala pada pukul 19.00, 19.30, 20.00, 20.30, atau 21.00 secara acak. Lampu tersebut kemudian akan otomatis padam pada suatu waktu antara pukul 04.00 sampai pukul 06.00 pagi harinya. Misalkan diketahui pada malam ini lampu tersebut menyala selama $t$ jam, peluang bahwa lampu menyala selama $9 < t < 10$ jam adalah …
- Untuk suatu bilangan bulat positif $n$, didefinisikan $B(n)$ sebagai bilangan bulat terkecil yang habis dibagi oleh semua bilangan bulat $1, 2, …, n$. Sebagai contoh, $B(5) = 60$, karena 60 habis dibagi oleh 1, 2, 3, 4, serta 5. Untuk $1 \le n \le 25$, banyaknya kemungkinan $n$ yang memenuhi $B(n) = B(n + 2)$ adalah …
- Misalkan $g(n)$ menyatakan faktor ganjil terbesar dari suatu bilangan bulat $n$. Sebagai contoh, $g(10) = 5, g(11) = 11$, dan $g(16) = 1$. Jika hasil penjumlahan $g(2019) + g(2020) + g(2021) + ⋯ + g(4038)$ adalah $2019 \text{×} m$, maka nilai $m$ adalah …
- Perhatikan kombinasi tiga lingkaran dan satu segitiga sama sisi berikut.
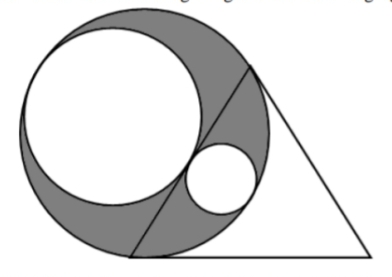
Jika diketahui luas daerah segitiga sama sisi adalah $4\sqrt{3}$ $cm^2$ dan luas daerah yang diarsir adalah $api$ $cm^2$, maka nilai $a$ adalah … $cm^2$. - Maman dan Nyoman secara terpisah dimintai untuk mewarnai suatu ornamen yang terlihat seperti gambar berikut.

Adapun ketentuan pewarnaan yang harus dipenuhi adalah setiap bintang harus diberi tepat satu warna dengan pilihan merah, kuning, atau hijau dan harus ada setidaknya 3 bintang yang berurutan yang berwarna hijau. Peluang pewarnaan yang dilakukan oleh Maman berbeda dengan pewarnaan yang dilakukan oleh Nyoman adalah … - Di babak bonus suatu kuis, seorang peserta akan diminta untuk mengambil secara acak 5 dari 20 bola yang telah dinomori 1 sampai 20. Hadiah utama akan didapatkan jika selisih nomor dari setiap pasang bola tidak kurang dari 3. Banyaknya kemungkinan peserta tersebut memenangkan hadiah utama adalah …
B. SOAL URAIAN
- Misalkan $f(5x + 2) \ge f(5x) + 2$ dan $f(5x + 1) \le f(5x) + 1$ untuk setiap bilangan $x$.Jika $g(x) = f(x) − 2$ dan $$f(5) =\frac{1}{(1)(2)}+\frac{1}{(2)(3)}+\frac{1}{(3)(4)}+\frac{1}{(4)(5)}+ ⋯ +\frac{1}{(2018)(2019)}$$ hitunglah nilai dari $g(7)$.
- Misalkan diketahui alfabet di suatu “Negeri Awan” hanya terdiri dari huruf A, B, C, D, dan E saja. Perhatikan bahwa A dan E adalah huruf vokal, sedangkan B, C, dan D adalah huruf konsonan. Suatu deretan huruf disebut kata jika tidak mengandung huruf sama bersebelahan serta tidak mengandung huruf vokal bersebelahan. Tentukan banyaknya kata di “Negeri Awan” yang terdiri dari 7 huruf.
- Sandi memiliki 12 kandang hamster yang terdiri dari 3 kandang warna hijau, 3 warna merah, 3 warna biru, dan 3 warna kuning. Terdapat 10 ekor hamster yang akan didistribusikan ke dalam kandang-kandang tersebut. Ia mendistribusikan 4 hamster ke dalam kandang warna hijau. Selanjutnya, ia mendistribusikan 3 hamster ke kandang warna merah, 2 hamster ke kandang warna biru, serta seekor hamster ke dalam kandang warna kuning. Asumsikan masing-masing hamster memiliki kemungkinan yang sama untuk dimasukkan ke dalam kandang tertentu. Tentukan peluang bahwa kandang hijau berisi lebih banyak hamster dibanding kandang lain, baik kandang hijau yang sewarna, maupun kandang lain warna.
