- Diketahui $x$ dan $y$ adalah dua bilangan bulat positif. Banyak $(x,y)$ sehingga kelipatan persekutuan terkecil dari $x$ dan $y$ sama dengan $2^{3}3^{5}5^{7}$ adalah …
- Jika $A = \{a, b, c\}$ dengan $a, b$, dan $c$ merupakan bilangan asli lebih besar daripada 1, serta $a\text{ x }b\text{ x }c = 180$ , maka banyak himpunan $A$ yang mungkin adalah …
- Bentuk sederhana dari ekspresi $\sqrt[3]{5}\left( \sqrt[3]{\frac{16}{25}}-\sqrt[3]{\frac{4}{25}}+\sqrt[3]{\frac{1}{25}} \right)^{-1}$ adalah …
- Diketahui $n_{1}=1$ dan $n_{k+1}=\frac{1}{1+\frac{1}{n_{k}}}$ untuk $n\in \{ 1,2,3,…,2016 \}$.
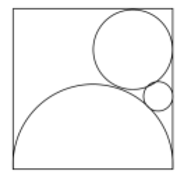
- Diberikan persegi dengan setengah lingkaran $L_{1}$, yang berpusat pada titik tengah alasnya. Lingkaran $L_{2}$, dengan radius $r$ menyinggung sisi atas dan sisi tegak persegi, serta $L_{1}$. Sedangkan lingkaran $L_{3}$ dengan radius $s$ menyinggung $L_{1}, L_{2}$, dan sisi tegak persegi. Rasio dari $r : s$ adalah …
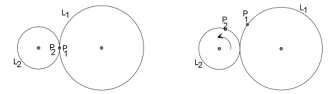
- Dua lingkaran $L_{1}$ dan $L_{2}$ mempunyai radius berturut-turut 12 cm dan 5 cm. Titik $P_{1}$ pada $L_1$ dan titik $P_2$ pada $L_2$. Mula-mula $L_1$ dan $L_2$ bersinggungan luar di $P_1$ dan $P_2$. Kemudian $L_2$ digelindingkan sepanjang $L_1$, sehingga tetap bersinggungan luar. Titik $P_2$ pertama kali bertemu kembali dengan $P_1$ ketika $L_2$ telah digelindingkan sebanyak … kali.
- Bilangan 3 angka yang habis dibagi 3 dengan semua angka penyusunnya merupakan anggota dari $S = \{2,3,5,6,7,9\}$ ada sebanyak …
- Sekolah $A$ memiliki 3 kelas yang akan mengikuti ujian komputer pada sekolah $B$. Sekolah $B$ menyediakan 2 pilihan waktu setiap harinya selama 5 hari berturut-turut. Setiap waktu yang disediakan dibuka dua kelas paralel. Jika setiap kelas sekolah $A$ hanya mengikuti satu kali ujian, dan waktu ujian ditentukan secara acak, maka peluang bahwa tiga kelas tersebut mengikuti ujian pada hari yang berbeda adalah …
Keranjang Belanja
