A. ISIAN SINGKAT
- Sebuah silinder memiliki tingggi 5 cm dan volume 20 $cm^2$. Luas permukaan bola terbesar yang mungkin diletakkan dalam silinder tersebut adalah …
- Jumlah tiga buah bilangan adalah 19. Jika bilangan pertama dan bilangan kedua masing-masing dikurangi 1, maka diperoleh dua bilangan dengan rasio 1 : 3. Jika bilangan kedua dan bilangan ketiga masing-masing ditambah 3, maka diperoleh dua bilangan dengan rasio 5 : 6. Selisih bilangan terbesar dan terkecil adalah …
- Jika $1+\frac{1}{4}+\frac{1}{9}+\frac{1}{16}+\frac{1}{25}+…=a$, maka $\frac{1}{9}+\frac{1}{25}+\frac{1}{49}+…$ = …
- Lima belas bilangan prima pertama dituliskan berturut-turut pada lima belas kartu. Jika semua kartu tersebut diletakkan dalam sebuah kotak dan kemudian diambil secara acak dua buah kartu berturut-turut tanpa pengembalian, maka peluang terambil dua kartu dengan jumlah dua bilangan yang tertulis merupakan bilangan prima adalah …
- Perhatikan gambar bangun datar setengah lingkaran dengan diameter $AD$ dan pusat lingkaran $M$ berikut. Misalkan $B$ dan $C$ adalah titik-titik pada lingkaran sedemikian sehingga $AC\bot BM$ dan $BD$ memotong $AC$ di titik $P$. Jika besar $angle CAD=s\circ$, maka besar sudut $\angle CPD$ = …
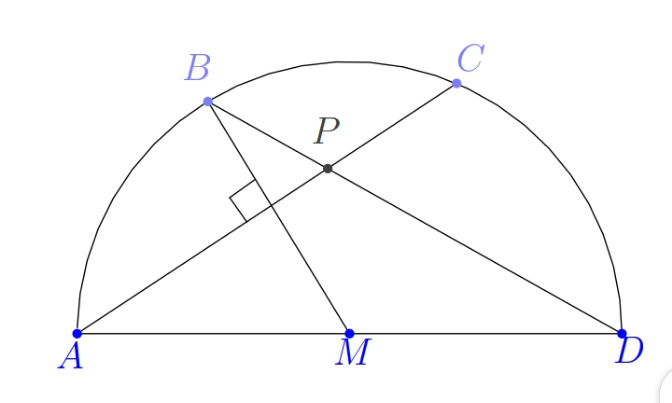
- Lima angka yakni 1, 2, 3, 4 dan 5 dapat disusun semuanya tanpa pengulangan menjadi 120 bilangan berbeda. Jika bilangan-bilangan tersebut diurutkan dari yang terkecil ke yang terbesar, maka bilangan yang menempati urutan ke-75 adalah …
- Diketahui $1+k$ habis dibagi 3, $1+2k$ habis dibagi 5, dan $1+8k$ habis dibagi 7. Jika $k$ adalah bilangan bulat positif maka nilai terkecil untuk $k$ adalah …
- Jika $p=2010^2+2011^2$ dan $q=2012^2+2013^2$, maka nilai sederhana dari $\sqrt{1-2(p+q)+4pq}$ adalah …
- Jika $a$ dan $b$ adalah penyelesaian dari persamaan kuadrat $4x^2-7x-1=0$, maka nilai dari $\frac{3a^2}{4b-7}+\frac{3b^2}{4a-7}$ adalah …
- Pada gambar berikut, kedua ruas garis putus-putus yang sejajar membagi persegi menjadi tiga daerah yang luasnya sama. Jika jarak kedua garis putus-putus tersebut adalah 1 cm, maka luas persegi adalah … $cm^2$.
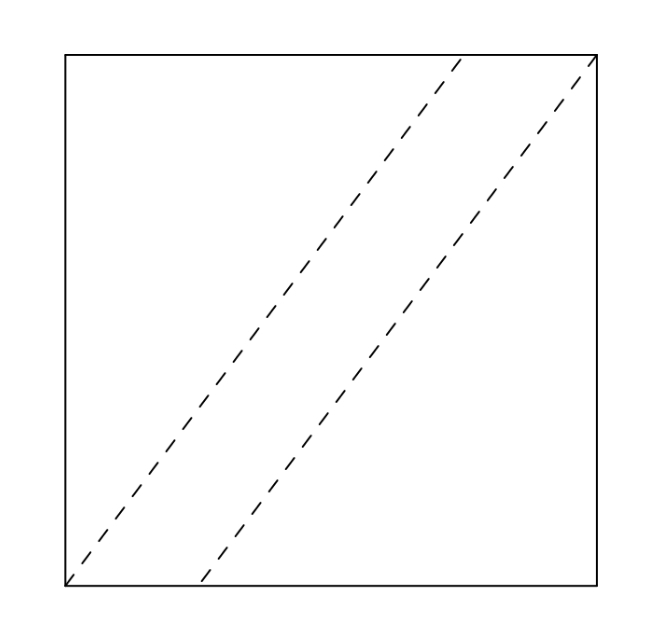
B. SOAL URAIAN
- Tentukan semua bilangan real $x$ yang memenuhi persamaan berikut: $$2^x+3^x-4^x+6^x-9^x=1$$
- Pada gambar berikut, sembilan lingkaran kecil dalam lambang olimpiade akan diisi masing-masing dengan bilangan 1, 2, 3, 4, 5, 6, 7, 8 atau 9. Tentukan pengisian tersebut sehingga jumlah bilangan di dalam setiap lingkaran besar adalah 14.
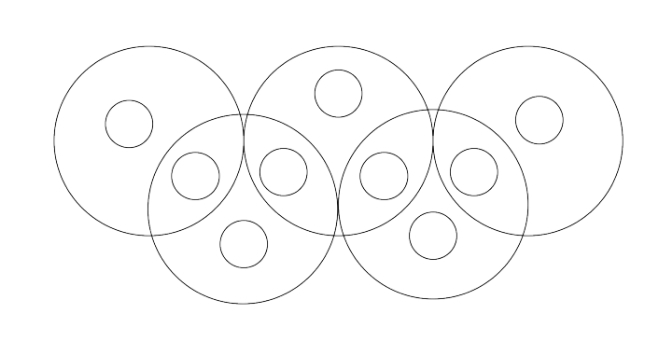
- Diketahui $\Delta ABC$ dengan $AB=$ 25 cm, $BC=$ 20 cm dan $AC=$ 15 cm. Jika titik $D$ terletak pada sisi $AB$ sedemikian sehingga perbandingan luas $\Delta ADC$ dan $\Delta ABC$ adalah 14 : 25, Tentukan panjang $CD$.
- Dari hasil sensus diketahui bahwa penduduk suatu kota tak lebih dari 1000 orang dan anak-anak 20% lebih banyak daripada penduduk dewasa. Jika anak laki-laki 10% lebih banyak daripada anak perempuan, serta diantara penduduk dewasa terdapat 15% lebih banyak perempuan. Tentukan jumlah terbesar yang mungkin dari penduduk kota tersebut.
- Diketahui sebuah bilangan rasional positif kurang dari 1 yang dinyatakan dalam pecahan biasa dalam bentuk paling sederhana. Jika kali pembilang dan penyebut dari bilangan rasional tersebut adalah $20!=1\cdot 2\cdot 3\cdot 4\cdot \cdot \cdot 20$. Tentukan semua bilangan yang dimaksud.
