A. ISIAN SINGKAT
- Jika $x$ adalah jumlah 99 bilangan ganjil terkecil yang lebih besar dari 2011 dan $y$ adalah jumlah 99 bilangan genap terkecil yang lebih besar dari 6, maka $x+y$ = …
- Jika $f$ adalah fungsi sehingga $f(xy)=f(x-y)$ dan $f(6)=1$, maka $f(-2)-f(4)$ = …
- Jika bilangan bulat $x$ dan $y$ dibagi 4, maka bersisa 3. Jika bilangan $x-3y$ dibagi 4, maka bersisa …
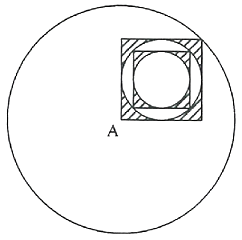
- Perhatikan gambar berikut. Suatu lingkaran berjari-jari 2 satuan berpusat di $A$. Suatu persegi memiliki titik sudut di $A$ dan satu titik sudut yang lain di lingkaran. Di dalam persegi tersebut terdapat lingkaran yang menyinggung keempat sisi persegi. Di dalam lingkaran terdapat persegi yang keempat titik sudutnya berada dilingkaran tersebut. Di dalam persegi ini terdapat lingkaran yang menyinggung keempat sisi persegi. Luas daerah yang diarsir sama dengan …
- Banyak bilangan 3 digit (angka) yang terdiri dari angka-angka 0, 2, 3, 5, 7, 8 yang lebih dari 243 dan kurang dari 780 adalah …
- Diketahui Budi adalah seorang siswa laki-laki dan Wati adalah seorang siswa perempuan. Saat ini mereka duduk di kelas IX pada suatu sekolah. Mereka mencatat banyak siswa kelas IX di sekolah mereka. Wati mencatat, 3/20 dari total siswa di kelas IX adalah laki-laki. Sedangkan menurut catatan Budi, 1/7 dari total siswa di kelas IX di sekolah mereka adalah …
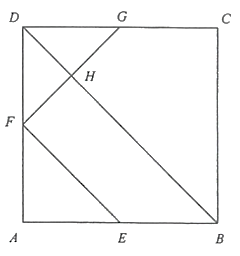
- Diketahui luas persegi $ABCD$ adalah 25 $m^{2}$. Jika $E, F$ dan $G$ masing-masing adalah titik tengah $AB, AD$ dan $CD$ seperti pada gambar berikut, maka luas trapesium $BHFE$ adalah … $m^{2}$.
- Tiga bilangan $a, b$ dan $c$ dipilih sehingga ketika setiap bilangan ditambahkan ke rata-rata dua bilangan lainnya maka berturut-turut hasilnya adalah 80, 90 dan 100. Rata-rata dari $a,b$ dan $c$ adalah …
- Sebuah bilangan bulat $x$ diambil secara acak dari $\{x|-5\le x \le 10, x\text{ bilangan bulat}\}$. Peluang bahwa $x$ adalah penyelesaian pertidaksamaan $\sqrt{x^{2}-3x\le 2}$ adalah …
- Misalkan $n$ adalah suatu bilangan asli dan $x$ adalah suatu bilangan riil positif. Jika $2x^{n}+\frac{3}{x^{-\frac{n}{2}}}-2=0$, maka nilai $\frac{2}{x^{n}+\frac{1}{4}}$ sama dengan …
B. SOAL URAIAN
- Saat ini umur Agus dan umur Fauzan kurang dari 100 tahun. Jika umur Agus dan umur Fauzan ditulis secara berurutan, maka diperoleh suatu bilangan empat digit (angka) yang merupakan kuadrat sempurna. Dua puluh tiga tahun kemudian, jika umur mereka ditulis dengan cara yang sama, maka diperoleh bilangan empat digit lain yang juga merupakan kuadrat sempurna. Jika umur mereka diasumsikan merupakan bilangan positif, berapakah umur mereka saat ini?
- Pada sebuah segiempat $ABCD$, sudut $ABC$ dan sudut $DAC$ adalah sudut siku-siku. Jika keliling segiempat $ABCD$ adalah 64 cm, keliling $ABC$ adalah 24 cm, dan keliling $ACD$ adalah 60 cm, berapakah luas segiempat $ABCD$?
- Diketahui bilangan bulat positif $n$ memiliki sifat-sifat berikut. 2 membagi $n$, 3 membagi $n+1$, 4 membagi $n+2$, 5 membagi $n+3$, 6 membagi $n+4$, 7 membagi $n+5$ dan 8 membagi $n+6$. Bilangan bulat positif pertama yang memiliki sifat-sifat ini adalah 2. Tentukan bilangan bulat positif ke-5 yang memenuhi sifat-sifat diatas!
- Tiga garis lurus $l_{1}, l_{2}$ dan $l_{3}$ mempunyai gradien berturut-turut 3, 4 dan 5. Ketiga garis tersebut memotong sumbu $Y$ di titik yang sama. Jika jumlah absis titik potong masisng-masing garis dengan sumbu $X$ adalah $\frac{47}{60}$, tentukan persamaan garis $l_{1}$.
- Data akhir suatu kompetisi yang diikuti oleh tiga tim sepakbola, masing-masing tim saling berhadapan, dituliskan pada berikut.
Berapakah skor pertandingan antara Tim Garuda melawan Tim Merpati?