- Izza menulis suatu bilangan bulat positif. Bilangan tersebut memberikan sisa 181 jika dibagi oleh 2024. Tentukan sisa pembagian bilangan tersebut oleh 88.
- Misalkan $x_1, x_2, x_3, … , x_{22}$ adalah barisan aritmetika yang hasil penjumlahan dari semua suku-sukunya adalah 2024. Diketahui $A = x_1 + x_3 + ⋯ + x_{21}$ dan $B = x_2 + x_4 + ⋯ + x_{22}$ dengan $A ∶ B = 11 ∶ 12$. Tentukan selisih nilai suku terbesar dan suku keempat dari barisan aritmetika tersebut.
- Perhatikan gambar segitiga ABC berikut.
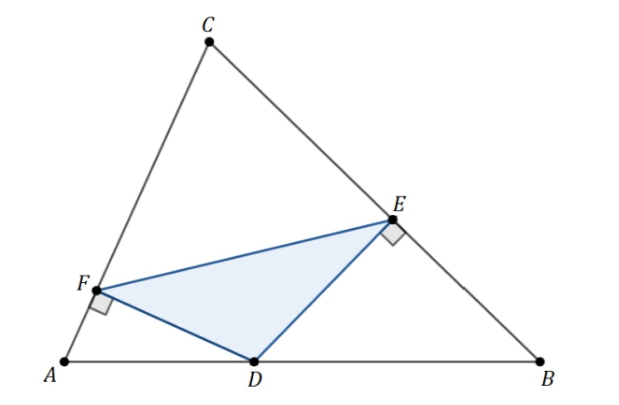
Panjang sisi BC = 12 cm dan AC = 8 cm. Titik $D, E$ dan $F$ berada pada sisi $AB, BC$ dan $AC$. Jika $DE$ = 4 cm, $AD: AB$ = 1: 3, serta $\angle DEB$ dan $\angle DFA$ adalah sudut siku-siku, tentukan luas daerah segitiga $DEF$. - Andi akan bertanding catur dengan Budi dan Cakra. Pertandingan dilakukan sampai ada pemenang (tidak ada hasil remis/seri). Andi mendapatkan hadiah jika ia memenangkan dua pertandingan berturut-turut dari tiga pertandingan yang dimainkan.
Terdapat dua skenario pertandingan yang dapat dipilih Andi seperti pada tabel berikut.
Andi tahu bahwa Budi bermain lebih baik daripada Cakra. Jelaskan secara matematis skenario mana yang memberikan peluang lebih besar bagi Andi untuk mendapat hadiah. - Sebuah meja karambol berbentuk persegi dengan sisi dalam 50 cm memiliki permukaan yang dibagi menjadi empat kuadran dengan warna berbeda, yaitu merah, hijau, kuning, dan biru. Sebuah cakram permainan berbentuk lingkaran berjari-jari 5 cm ditempatkan secara acak ke atas meja tersebut. Tentukan peluang bahwa cakram tersebut tepat menempati tiga daerah dengan warna berbeda.
Berikut adalah salah satu contoh posisi cakram yang dimaksud.
- Dalam babak bonus suatu kuis, seorang pemain diminta menekan tombol yang akan menampilkan secara acak dua bilangan bulat positif yang kurang dari 100 di layar. Ia akan mendapatkan hadiah utama jika jumlah dan hasil kali kedua bilangan yang tampil adalah bilangan kuadrat. Tentukan banyaknya kemungkinan ia mendapatkan hadiah utama.
- Didefinisikan bilangan Salas adalah bilangan tiga angka yang dapat dinyatakan dalam bentuk $\pm \overline{abc}$ x $10^n$ dengan $n \in {−2, −1,0}$. Jika $f(x) = 2x^3 − x^2 − 6x + 3$, maka tentukan semua bilangan Salas $x$ yang memenuhi $−0,02 < f(x) < −0,01$.
- Panjang salah satu rusuk dari suatu balok adalah $7 + \sqrt{3}$ cm dan luas permukaannya 176 $cm^2$. Volume balok adalah V $cm^3$ dan total panjang rusuk adalah $k$ cm, dengan $V$ dan $k$ merupakan bilangan bulat.
Tentukan panjang diagonal ruang balok tersebut. - Diberikan himpunan $S = \{0, 1, 2, … , 9\}$. Himpunan bagian dari $S$ disebut Matsik jika memiliki setidaknya 3 anggota. Akan dipilih satu Matsik secara acak. Tentukan peluang terpilihnya Matsik yang memiliki setidaknya dua anggota kelipatan 3 dan hasil penjumlahan seluruh anggotanya juga merupakan kelipatan 3.
- Seorang perancang bangunan merancang jembatan gantung sepanjang 120 meter dan lebar 5 meter menggunakan lima pasang tiang gantung dengan rancangan tampak depan (satu sisi) seperti gambar berikut.

Pada satu sisi depan, jembatan berada 2 meter di atas permukaan air. Tinggi tiang gantung yang diukur dari atas permukaan air masing-masing $BL$ = 4 m, $CM$ = 20 m, $DN$ = 4 m, $EO$ = 8 m, dan $FP$ = 4 m. Kawat penyangga $KLM$ dan $MNO$ berbentuk parabola, sedangkan $OPQ$ berbentuk garis. Jarak titik $K$ ke tiang $BL$ adalah 20 m dan jarak titik $Q$ ke tiang $FP$ adalah 10 m.
Untuk menahan jembatan, disusun tali-tali yang menggantung dan diikat pada kawat penyangga $KLMNOPQ$ dan pinggir jembatan dengan jarak antar tali adalah 1 meter. Diasumsikan bahwa panjang tali yang digunakan adalah panjang tali dari kawat penyangga ke pinggir jembatan dan tegak lurus terhadap jembatan. Apabila harga tali per meter adalah Rp100.000, hitunglah biaya total tali yang diperlukan untuk kedua sisi jembatan tersebut.
Keranjang Belanja
