- Sebuah persegi dibagi menjadi 2 persegi panjang seperti terlihat pada gambar. Diketahui hasil penjumlahan kedua keliling persegi panjang tersebut adalah 60, maka luas persegi adalah …

- Diketahui ada 6 pilihan jalan yang dapat digunakan untuk berpergian dari kota A ke kota B dan ada 8 pilihan jalan yang dapat digunakan untuk berpergian dari kota B ke kota C, Jika seseorang akan berpergian dari kota A ke kota C melalui kota B dan pulang kembali lagi ke kota A melalui jalan jalan yang berbeda dari ketika saat pergi, banyaknya cara memilih jalan yang dapat dilalui adalah …
- Pada papan tertulis 90 bilangan asli 1,1,..,1,a,b (ada sebanyak 88 bilangan 1). Hasil penjumlahan seluruh bilangan di papan adalah A dan demikian juga hasil perkalian semua bilangan di papan adalah A. Nilai A adalah …
- Misalkan $a,b$ bilangan bulat positif yang tidak memiliki faktor persekutuan positif selain 1. Jika berlaku $\frac{1+2+3+…+104}{3+4+5+…+106}=\frac{a}{b}$, maka nilai $a+b$ adalah …
- Bilangan OSK adalah bilangan 4 angka yang tidak di mulai dengan angka 0 dan hasil penjumlahan semua digitnya adalah 8. Sebagai contoh, 2024 merupakan bilangan OSK. Banyaknya bilangan OSK adalah …
- Misalkan $u_{1},u_{2},u_{3},…$ suatu barisan geometri dengan $u_{1}>u_{2}$. Jika $u_{2}=8$ dan $u_{5}+u_{7}=\frac{17u_{6}}{4}$. Nilai dari $u_{1}$ adalah …
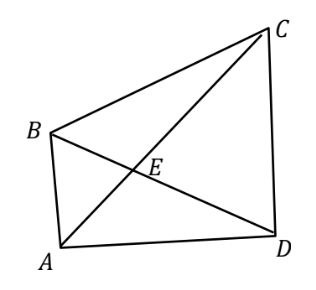
- Diberikan segiempat $ABCD$ dengan luas segitiga $AED$ sama dengan luas segitiga $BEC$. Jika $AB=50$, $AE=45$ dan $AC=108$, maka $CD$ adalah …
- Banyaknya bilangan dua digit $\overline{ab}$ dengan $a$, $b \neq 0$ sehingga $\overline{ab} + \overline{ba}$ merupakan bilangan kelipatan 66 adalah …
- Misalkan $k$ adalah bilangan bulat positif terkecil kelipatan 2024 yang memiliki 28 faktor positif. Sisa hasil bagi $k$ oleh 100 adalah …
- Misalkan $x,y$ bilangan real positif dengan $x>y$. Jika diketahui bahwa $x^{2}+y^{2}=(\frac{545}{272})xy$, maka $\frac{x+y}{x-y}$ adalah …
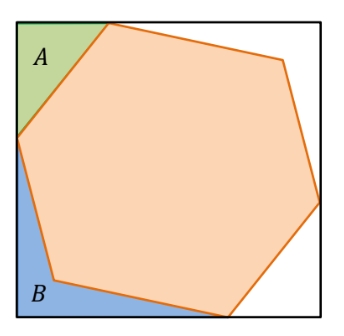
- Suatu segienam beraturan disisipkan kedalam sebuah persegi panjang seperti terlihat pada gambar dibawah ini, jika luas $A$ dan $B$ berturut-turut adalah 24 dan 23, maka luas segienam beraturan adalah …
- Banyak himpunan bagian $A$ dari $\{24,25,26,…,35\}$ sehingga hasil penjumlahan unsur terbesar dan terkecil dari $A$ sama dengan 59 adalah …
- Untuk setiap bilangan asli $n$, misalkan $f(n)$ menyatakan faktor ganjil terbesar dari $n$ dan $p(n)=f(n)+f(n+1)+…+f(2n)$. Jika $p(n)=8145$, maka $n$ adalah …
- Diberikan suku banyak $P(x)=x^{3}+Dx^{2}+Ex+1$ dan $P(-1)=4$. Jika $a,b,c$ merupakan akar-akar dari $P(x)=0$ dan memenuhi $(a^{2}-bc)(b^{2}-ca)(c^{2}-ab)=40$, Maka nilai dari $(D+E)^{2}$ adalah …
- Banyaknya barisan bilangan bulat positif dengan enam suku $a_{1},a_{2},a_{3},a_{4},a_{5},a_{6}$ yang mungkin sehingga $1 \le a_{1},a_{2},a_{3},a_{4},a_{5},a_{6} \le 4$ dan tidak ada dua suku berurutan yang jumlahnya 4 adalah …
- Diberikan sebuah segitiga $ABC$ yang siku-siku pada sudut $B$, Lingkaran $\omega$ merupakan lingkaran dalam segitiga $ABC$ yang menyinggung sisi $BC$ pada titik $D$. Titik $E$ terletak pada $\omega$ sehingga $PE$ merupakan diameter dari $\omega$. Perpanjangan garis $AE$ memotong $\omega$ kedua kalinya pada titik $F$, dan memotong sisi $BC$ pada titik $G$. Apabila $EF=3$ dan $FG=4$, maka panjang $AE$ dapat dinyatakan dalam bentuk $\frac{p}{r} \sqrt{q}$, dengan $p,q,r$ merupakan bilangan bulat positif, satu-satunya faktor kuadrat dari $q$ adalah 1 dan $FPB(p,r)=1$. Nilai dari $p+q+r$ adalah …
- Diketahui $a,b,c$ bilangan real positif yang memenuhi $a+b+c=\frac{32}{a}+\frac{32}{b}+\frac{32}{c}=24$. Nilai terbesar yang mungkin dicapai oleh $\frac{a^{2}+32}{a}$ adalah …
- Untuk setiap bilangan real $x$, notasi $\left\lfloor x\right\rfloor$ menyatakan bilangan bulat terbesar yang kurang dari atau sama dengan $x$. Sebagai contoh $\left\lfloor 1,1 \right\rfloor =1, \left\lfloor 3 \right\rfloor= 3$ dan sebagainya. Jika ada tepat sebanyak 1000 bilangan berbeda pada barisan $$\left\lfloor \frac{1^{2}}{2024} \right\rfloor,\left\lfloor \frac{2^{2}}{2024} \right\rfloor,\left\lfloor \frac{3^{2}}{2024} \right\rfloor,…,\left\lfloor \frac{n^{2}}{2024} \right\rfloor$$ maka $n$ = …
- Banyaknya pemetaan $f:\{1,2,3,4,5\}\to \{1,2,3,4,5\}$ sehingga $f(f(x))\in \{2,4\}$ untuk setiap $x \in \{1,2,3,4,5\}$ adalah …
- Pada $\Delta ABC$, titik $D$ dan $E$ terletak pada sisi $BC$ sehingga $B,D,E,C$ terletak pada urutan tersebut. Diketahui bahwa $BD:DE:EC =4:2:5$ dan garis-garis $AD$ dan $AF$ membagi tiga $\angle BAC$ sama besar. Garis $AD$ dan $AE$ masing-masing memotong lingkaran luar $\Delta ABC$ pada titik $F$ dan $G$. Nilai dari $\frac{DF}{EG}$ dapat dinyatakan dalam bentuk $\sqrt{\frac{p}{q}}$ untuk suatu bilangan bulat positif $p$ dan $q$ yang saling relatif prima, nilai dari $p+q$ adalah …
Keranjang Belanja
