- Hasil penjumlahan semua solusi persamaan $$|x-|2x+3||=99$$ adalah …
- Didalam suatu laci terdapat tujuh pasang kaos kaki yang setiap pasangannya berbeda dengan pasangan lainnya. Diambil lima kaos kaki sekaligus secara acak. Banyaknya cara pengambilan sehingga di antara yang terambil tedapat tepat sepasang kaos kaki yang cocok (berpasangan) adalah …
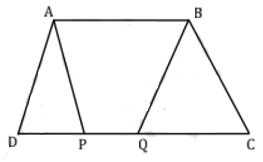
- Diberikan trapesium $ABCD$ dengan $AB =14, CD =19$. $AB$ sejajar $CD$, dan kedua sudut $\angle ADC$ dan $\angle BCD$ lancip. Misalkan $P$ dan $Q$ titik yang terletak pada sisi $CD$ sehingga $AD = AP$ dan $BC =BQ$. Panjang $PQ$ = …
- Suatu bilangan 4 digit $\overline{7ab9}$ merupakan suatu bilangan kuadrat. Nilai $a+b$ adalah …
- Diberikan fungsi kuadrat $f(x) = ax^{2} + bx =c$ yang memenuhi $f(5)=25$ dan $f(6) =36$. Jika $a \neq 1$, maka nilai dari $\frac{c-b}{a-1}$ adalah …
- Dua tim A dan B bertanding sepak bola sebanyak 15 kali. Pada setiap pertandingan, tim yang berhasil mencetak 4 gol pertama menjadi pemenang dan tidak ada pertandingan yang berakhir seri. Selama 15 pertandingan tersebut, tim A memenangkan pertandingan lebih banyak dibandingkan tim B, namun banyak gol yang dicetak tim B lebih banyak lebih banyak dibandingkan tim A. Selisih total gol terbesar yang mungkin di cetak kedua tim tersebut adalah …
- Diberikan segitiga lancip $ABC$ dengan $AB = 12$ dan $AC = 10$ dan $D$ suatu titik pada sisi $BC$. Misalkan $E$ dan $F$ menyatakan titik-titik berat segitiga $ABD$ dan $ACD$, Jika luas segitiga $DEF$ adalah 4, maka panjang sisi $BC$ adalah $\sqrt{n}$ dengan $n$ = …
- Sisa pembagian bilangan $5^{2022}+11^{2022}$ oleh 64 adalah …
- Diberikan suku banyak $P(x)$ dengan koefisien bulat jika $$P(r_{1})=P(r_{2})=200$$ dengan $r_{1},r_{2}$ merupakan akar-akar persamaan $x^{2}+x-23=0$, maka sisa pembagian $P(1)$ oleh 21 adalah …
- Banyaknya bilangan 4 digit yang habis dibagi 3 dan memuat angka 6 adalah …
- Misalkan $ABCD$ segiempat tali busur dengan lingkaran luar $\omega$ dan $BC=CD$. Diagonal $AC$ dan $BD$ berpotongan dititik $E$ dan diketahui bahwa $BE=7$ dan $DE=5$. Jika garis singgung $\omega$ dititik $A$ memotong perpanjangan diagonal $BD$ dititik $P$, maka $\frac{PD}{PB}$ dapat dituliskan dalam bentuk $\frac{m}{n}$ dengan $m,n$ bialngan asli yang relatif prima. Nilai dari $m+n$ adalah …
- Jika bilangan asli $x$ dan $y$ memenuhi persamaan $$x(x-y)=5y-6$$ maka $x+y$ = …
- Misalkan $a_{1},a_{2},a_{3},…$ suatu barisan bilangan yang memenuhi persamaan $$a_{n+2}-a_{n+1}+a_{n}=\frac{n+1}{6}$$ untuk setiap bilangan asli $n$. Jika $a_{1}=1$ dan $a_{2}=2$, maka $a_{2023}$ = …
- Diberikan himpunan $S=\{a,b,c,d,e,f\}$. Akan dipilih dua sub himpunan dari $S$ yang gabungannya adalah $S$. Sub himpunan yang dipilih tidak harus berbeda, misalnya keduanya boleh sama dengan $S$. Urutan dari sub himpunan yang dipilih tidak diperhatikan, sebagai contoh pasangan sub himpunan $(\{a,b,c\},\{c,d,e,f\})$ sama dengan pasangan $(\{c,d,e,f\}\{a,b,c\})$. Banyaknya cara melakukan pemilihan adalah …
- Diberikan lingkaran $\Omega$ dan $AB$ suatu tali busur dari $\Omega$. Lingkaran $\omega_{1}$ menyinggung $\Omega$ secara internal dan menyinggung $AB$ pada titik tengahnya. Lingkaran $\omega_{2}$ menyinggung $\Omega$ secara internal, menyinggung $\omega_{1}$, secara eksternal dan juga menyinggung $AB$.
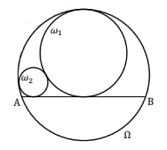
Jika jari-jari $\omega_{1}$ adalah 35 dan jari-jari $\omega_{2}$ adalah 7, maka panjang $AB$ adalah … - Misalkan $n=2^{a}3^{b}$ dengan $a$ dan $b$ bilangan asli. Jika hasil kali semua faktor positif dari $n$ adalah $12^{90}$, maka nilai $ab$ = …
- Nilai minimum dari $$\frac{(x+y)^{2}}{\sqrt{x^{2}-16}+\sqrt{y^{2}-25}}$$ adalah …
- Diberikan 100 titik seperti gambar dibawah ini. Banyaknya persegi yang semua titik sudutnya adalah empat titik di antara titik-titik pada gambar adalah …

- Diberikan segitiga $ABC$. Misalkan $D,E,F$ masing-masing adalah titik pada sisi $BC,CA,AB$ sehingga $AD,BE,CF$ berpotongan di satu titiik. Diketahui bahwa $\angle EDF = 54\circ$. Jika $\angle ADB = 90\circ$ dan $AF=FB$, maka besar sudut $\angle ABC$ = …
- Misalkan $p$ dan $n$ dua bilangan asli dengan $p$ bilangan prima sedemikian sehingga $p$ membagi $n^{2}+4$ dan $n$ membagi $p^{2}+4$. Jika $p<200$, maka nilai terbesar yang mungkin dari $n$ adalah …
Keranjang Belanja
