- Jumlah dari semua bilangan real $x$ yang memenuhi $$x^2 − 2x = 2 + x\sqrt{x^2 − 4x}$$ adalah …..
- Banyaknya bilangan bulat $n$, sehingga $n + 1$ merupakan faktor dari $n^2 + 1$ adalah …..
- Dalam suatu pesta, setiap pria berjabat tangan dengan pria lain hanya sekali. Demikian juga, setiap wanita hanya berjabat tangan sekali dengan wanita lain yang hadir dalam pesta tersebut. Tidak ada yang berjabat tangan antara pria dan wanita dalam pesta tersebut. Jika banyaknya pria yang hadir dalam pesta lebih banyak dari wanita dan jumlah jabat tangan antara pria atau wanita ada 7 jabat tangan. Banyaknya pria yang hadir dalam pesta tersebut adalah ……
- Diberikan segitiga ABC, melalui titik D yang terletak pada sisi BC ditarik garis DE dan DF berturut-turut sejajar dengan AB dan AC, (E pada AC, F pada AB). Jika luas segitiga DEC sama dengan 4 kali luas segitiga BDF, maka perbandingan luas segitiga AEF dengan luas segitiga ABC adalah………
- Jika $f$ adalah fungsi yang terdefinisi pada himpunan bilangan real dan berlaku $$3f (x) − 2f (2 − x) = x^2 + 8x − 9$$ untuk semua bilangan real $x$, maka nilai dari $f(2015)$ adalah ……
- Banyaknya pasangan bilangan bulat (a, b) yang memenuhi $\frac{1}{a}+\frac{1}{b + 1}=\frac{1}{2015}$ adalah …….
- Ada 10 orang, lima laki-laki dan lima perempuan, termasuk sepasang pengantin. Seorang tukang foto yang bukan salah satu di antara 10 orang tersebut akan megambil gambar enam orang di antara mereka, termasuk ke-dua pengantin, dengan tidak ada dua laki-laki maupun dua perempuann yang berdekatan. Banyaknya cara adalah ……
- Panjang sisi-sisi segitiga merupakan bilangan bulat berurutan, dan sudut terbesar dua kali sudut terkecil. Nilai cosinus sudut terkecil adalah ………
- Diberikan dua suku banyak kuadrat berbeda $f(x) = x^2 + ax + b$ dan $g(x) = x^2 + cx + d$ yang memenuhi $$f(20) + f(15) = g(20) + g(15).$$ Jumlah dari semua bilangan real $x$ yang memenuhi $f(x) = g(x)$ sama dengan ……
- Diberikan $a$ dan $b$ bilangan bulat positif dengan $\frac{53}{201} < \frac{a}{b} < \frac{4}{15}$. Nilai $b$ terkecil yang mungkin adalah…….
- Misalkan pada suatu laboratorium terdapat 20 komputer dan 15 printer. Kabel digunakan untuk menghubungkan komputer dan printer. Sayangnya, satu printer hanya dapat melayani satu komputer pada suatu waktu bersamaan. Diinginkan 15 komputer selalu dapat menggunakan printer pada waktu bersamaan. Banyaknya kabel yang diperlukan untuk menghubungkan komputer dan printer minimal ada sebanyak ……
- Diberikan segitiga ABC dengan M pertengahan BC, dan pada sisi AB dipilih titik N sehingga NB = 2NA. Jika $\angle CAB = \angle CMN$, maka nilai dari $\frac{AC}{BC}$ adalah……
- Diberikan barisan $a_0, a_1, a_2,$ . . . dengan $a_0 = 2, a_1 = 83$ dan $$a_m ∙ a_n = a_{m+n} − a_{m−n}$$ untuk setiap bilangan asli $m, n$ dengan $m \ge n$. Banyaknya bilangan asli $n$ yang memenuhi $$a_n − 3^n > \frac{1}{2015}$$ adalah ……
- Untuk bilangan real $x$, notasi $⌊x⌋$ menyatakan bilangan bulat terbesar yang tidak lebih besar dari $x$; sedangkan $⌈x⌉$ menyatakan bilangan bulat terkecil yang tidak lebih kecil dari $x$. Bilangan real $x$ yang memenuhi $$⌊x⌋^2 − 3x + ⌈x⌉ = 0$$ adalah ……
- Suatu lingkaran memotong segitiga sama sisi ABC pada enam titik yang berbeda. Keenam titik komposisinya, setiap dua titik terletak pada sisi segitiga, sehingga: B, D, E, C; C, F, G, A, dan A, H, J, B berturut-turut segaris. Jika AG = 2, GF = 13, FC = 1, dan HJ = 7, maka panjang DE adalah …..
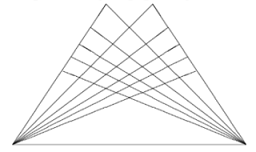
- Pada gambar terdapat segitiga sebanyak ……
- Misalkan M dan m berturut turut merupakan nilai a terbesar dan terkecil sehingga berlaku $|x^2 − 2ax − a^2 −\frac{3}{4}| \le 1$ untuk setiap $x \in$ [0, 1]. Nilai dari M − m adalah ……
- Semua bilangan bulat $n$ sehingga $\frac{9n + 1}{n + 3}$ merupakan kuadrat suatu bilangan rasional adalah …….
- Himpunan A bagian dari $\{1, 2, 3, … , 15\}$ dikatakan baik, jika untuk setiap $a \in A$ berlaku $a − 1 \in A$ atau $a + 1 \in A$. Banyaknya himpunan bagian dengan lima anggota dari $\{1, 2, . . . , 15\}$ yang baik ada sebanyak …….
- Diberikan segitiga sama kaki $ABC$, dengan $AB = AC = b, BC = a$, dan $\angle BAC = 100\circ$. Jika $BL$ garis bagi $\angle ABC$, maka nilai $AL + BL$ adalah ……
- Misalkan $X = \{1, 2, 3, 4, 5\}.$
Misalkan $F = \{A_1, A_2, A_3, . . . , A_m\}$, dengan $A_i \subseteq \text{X}$ dan anggota $A_i$ sebanyak 2, untuk $i = 1, 2, . . . , m$. Tentukan $m$ minimum sehingga untuk sebarang $B \subseteq \text{X}$, dengan $B$ beranggota sebanyak 3, terdapat anggota $F$ yang termuat di $B$. Buktikan jawab Anda. - Tentukan semua tripel bilangan real (x, y, z) yang memenuhi sistem persamaan $$(x + 1)^2 = x + y + 2$$ $$(y + 1)^2 = y + z + 2$$ $$(z + 1)^2 = z + x + 2.$$
- Diberikan segitiga samakaki ABC, dengan AB = AC. Misalkan D titik pada segmen BC sehingga BD = 2DC. Misalkan pula bahwa P titik pada segmen AD sehingga: $\angle BAC = \angle BPD$. Buktikan bahwa $\angle BAC = 2\angle DPC$.
- Misalkan $p_1, p_2, …, p_n$ barisan aritmetika dengan beda $b > 0$ dan $p_i$ prima untuk setiap $i = 1, 2, … , n.$
1. Jika $p_1 > n$, tunjukkan bahwa setiap bilangan prima $p$ dengan $p \le n$, maka $p$ membagi habis $b$.
2. Berikan contoh barisan aritmetika $p_1, p_2, … , p_{10}$, dengan beda positif dan $p_i$ prima untuk $i = 1, 2, … , 10$. - Diberikan himpunan yang terdiri 22 bilangan bulat, $A = {±a_1, ±a_2, . . . , ±a_{11}}$. Tunjukkan bahwa terdapat himpunan bagian S dari A yang sekaligus mempunyai sifat berikut:
1. Untuk setiap $i = 1, 2, … , 11$ paling banyak hanya satu di antara $a_i$ atau $−a_i$ merupakan anggota S
2. Jumlah semua bilangan di S habis dibagi 2015.
Keranjang Belanja
