- Misalkan $O$ dan $I$ berturut-turut menyatakan titik pusat lingkaran luar dan titik pusat lingkaran dalam pada segitiga dengan panjang sisi 3, 4 dan 5. Panjang dari $OI$ adalah ……
- Misalkan $x, y$ dan $z$ adalah bilangan-bilangan prima yang memenuhi persamaan $34x − 51y = 2012z$. Nilai dari $x + y + z$ adalah…
- Diketahui empat dadu setimbang dan berbeda, yang masing-masing berbentuk sisi delapan beraturan bermata 1, 2, 3, …, 8. Empat dadu tersebut ditos (dilempar) bersama-sama satu kali. Probabilitas kejadian ada dua dadu dengan mata yang muncul sama sebesar …
- Fungsi bernilai real $f$ dan $g$ masing-masing memiliki persamaan $$f(x) =\sqrt{⌊x⌋ − a} \text{ dan } g(x) = \sqrt{x^2} −\frac{x\sqrt{2}}{\sqrt{a}}$$ dengan $a$ bilangan bulat positif. Diketahui $⌊x⌋$ menyatakan bilangan bulat terbesar yang kurang dari atau sama dengan $x$. Jika domain $g$ $o$ $f$ adalah ${x|3\frac{1}{2}\le x < 4}$, maka banyaknya $a$ yang memenuhi sebanyak …..
- Diberikan bilangan prima $p > 2$. Jika $S$ adalah himpunan semua bilangan asli $n$ yang menyebabkan $n^2 + pn$ merupakan kuadrat dari suatu bilangan bulat, maka $S$ = …..
- Untuk sebarang bilangan real $x$ didefinisikan $\{x\}$ sebagai bilangan bulat yang terdekat dengan $x$, sebagai contoh $\{1,9\} = 2, \{0,501\} = 1$, dan sebagainya. Jika $n$ adalah suatu bilangan bulat positif kelipatan 2012, maka banyak bilangan bulat positif $k$ yang memenuhi ${\sqrt[3]{k} = n}$ adalah …..
- Banyak bilangan bilangan asli $n < 100$ yang mempunyai kelipatan yang berbentuk $$123456789123456789…123456789$$ adalah …..
- Diberikan jajar genjang $ABCD$. Titik $M$ pada $AB$ sedemikian rupa sehingga $\frac{AM}{AB}= 0,017$, dan titik $N$ pada $AD$ sehingga $\frac{AN}{AD}=\frac{17}{2009}$. Misalkan $AC \cap MN = P$, maka $\frac{AC}{AP}$ =
- Dalam sebuah pertemuan, 5 pasang suami istri akan didudukkan pada sebuah meja bundar. Berapa banyak cara untuk mengatur posisi duduk 5 pasang suami istri tersebut sedemikian sehingga tepat 3 suami duduk disamping istrinya?
- Jika $p, q$ dan $r$ akar-akar dari persamaan $x^3 − x^2 + x − 2 = 0$, maka $p^3 + q^3 + r^3$ = …..
- Jika $m$ dan $n$ bilangan bulat positif yang memenuhi persamaan $$m^2 + n^5 = 252,$$ maka $m + n$ = …..
- Pada $\Delta ABC$, titik $D$ terletak pada garis $BC$. Panjang $BC$ = 3, besar sudut $\angle ABC = 30\circ$, dan $\angle ADC = 45\circ$. Panjang $AC$ = …..
- Lima siswa, A, B, C, D, E berada pada satu kelompok dalam lomba lari estafet. Jika A tidak bisa berlari pertama dan D tidak bisa berlari terakhir, maka banyaknya susunan yang mungkin adalah …..
- Diketahui H adalah himpunan semua bilangan asli kurang dari 2012 yang faktor primanya tidak lebih dari 3: Selanjutnya didefnisikan himpunan $$S = {\frac{1}{n}| n \in H}$$. Jika $x$ merupakan hasil penjumlahan dari semua anggota $S$ dan $⌊x⌋$ menyatakan bilangan bulat terbesar yang kurang dari atau sama dengan $x$, maka $⌊x⌋$ = …..
- Diberikan dua lingkaran $R_1$ dan $R_2$ yang berpotongan di dua titik yaitu A dan B dengan AB = 10. Ruas garis yang menghubungkan titik pusat kedua lingkaran memotong lingkaran $R_1$ dan $R_2$ masing-masing di $P$ dan $Q$. Jika $PQ$ = 3 dan jari-jari lingkaran $R_1$ adalah 13, maka jari-jari lingkaran $R_2$ adalah …..
- Banyaknya pasangan bilangan bulat ($x, y$) yang memenuhi $$\frac{1}{x}+\frac{1}{y}−\frac{1}{xy^2} =34$$ adalah ……
- Untuk bilangan real positif $x$ dan $y$ dengan $xy =\frac{1}{3}$ nilai minimum dari $\frac{1}{9x^6}+\frac{1}{4y^6}$ adalah …..
- Banyaknya pasangan bilangan bulat positif ($a, b$) yang memenuhi $4^a + 4a^2 + 4 = b^2$ adalah ……
- Diberikan segitiga ABC, dengan panjang AB sama dengan dua kali panjang AC. Misalkan D dan E berturut-turut pada segmen AB dan BC,
sehingga $\angle BAE = \angle ACD$. Jika $F = AE \cap CD$ dan CEF merupakan segitiga sama sisi, maka besar sudut dari segitiga ABC adalah …… - Banyaknya bilangan bulat positif $n$ yang memenuhi $n \le 2012$ dan merupakan bilangan kuadrat sempurna atau kubik atau pangkat 4 atau pangkat 5 atau … atau pangkat 10, ada sebanyak ……
- Tentukan semua pasangan bilangan bulat tak negatif ($a, b, x, y$) yang memenuhi sistem persamaan $$ \left\{ \begin{array}{cl}
a+b& : xy \\
x+y & : ab
\end{array} \right.$$ - Cari semua pasangan bilangan real ($x, y, z$) yang memenuhi sistem persamaan.
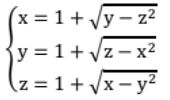
- Seorang laki-laki memiliki 6 teman. Pada suatu malam di suatu restoran, dia bertemu dengan masing-masing mereka 11 kali, setiap 2 dari mereka 6 kali, setiap 3 dari mereka 4 kali, setiap 4 dari mereka 3 kali, setiap 5 dari mereka 3 kali, dan semua mereka 10 kali. Dia makan diluar 9 kali tanpa bertemu mereka. Berapa kali dia makan di restoran tersebut secara keseluruhan?
- Diketahui segitiga lancip ABC. Titik H menyatakan titik kaki dari garis tinggi yang ditarik dari A. Buktikan bahwa $AB + AC \ge BC \cos \angle BAC + 2AH \sin \angle BAC$
- Diketahui $p_0 = 1$ dan $p_i$ bilangan prima ke-$i$, untuk $i$ = 1, 2, …; yaitu $p_1 = 2, p_2 = 3$. … Bilangan prima $p_i$ dikatakan sederhana jika $$p_i^{(n^2)} > p_{i−1}(n!)^4$$ untuk semua bilangan bulat positif $n$. Tentukan semua bilangan prima yang sederhana!
Keranjang Belanja
