- Diketahui bangun persegi panjang berukuran 4 × 6 dengan beberapa ruas garis, seperti pada gambar.
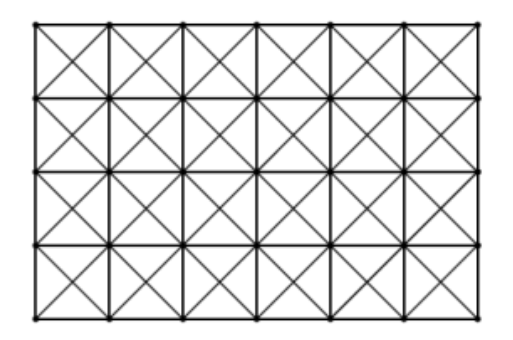
Dengan menggunakan ruas garis yang sudah ada, tentukan banyak jajaran genjang tanpa sudut siku-siku pada gambar tersebut ! - Diberikan segitiga lancip $ABC$ dengan lingkaran luar $\omega$. Garis bagi $\angle BAC$ memotong $\omega$ di titik $M$. Misalkan $P$ suatu titik pada garis $AM$ dengan $P$ di dalam segitiga $ABC$. Garis melalui $P$ yang sejajar $AB$ dan garis melalui $P$ yang sejajar $AC$ memotong sisi $BC$ berturut-turut di titik $E$ dan $F$. Garis $ME$ dan $MF$ memotong $\omega$ berturut-turut di titik $K$ dan $L$. Buktikan bahwa tiga garis $AM, BL$ dan $CK$ konkuren.
- Tentukan semua bilangan real positif $M$ sedemikian sehingga untuk sebarang bilangan real positif $a, b, c$ paling sedikit satu diantara tiga bilangan berikut $$a+\frac{M}{ab},b+\frac{M}{bc},c+\frac{M}{ca}$$ bernilai lebih dari atau sama dengan $1+M$.
- Misalkan $3 < p$ bilangan prima, dan $$S=\sum_{2\le i\lt j\lt k\le p-1}^{}ijk$$ Buktikan bahwa bilangan $S + 1$ habis dibagi $p$.
- Diberikan sebarang polinom kuadrat $P(x)$ dengan koefisien utama positif dan diskriminan negatif. Buktikan bahwa $P(x)$ dapat dinyatakan sebagai jumlah tiga polinom kuadrat $$P(x) = P_{1}(x) + P_{2}(x) + P_{3}(x)$$ dengan $P_{1}(x), P_{2}(x), P_{3}(x)$ memiliki koefisien utama positif dan diskriminan nol serta akar (real kembar) dari ketiga polinom tersebut berbeda.
- Bilangan asli $n$ dikatakan “kuat” jika terdapat bilangan asli $x$ sehingga $x^{nx} + 1$ habis dibagi $2^{n}$.
1. Buktikan bahwa 2013 merupakan bilangan kuat.
2. Jika $m$ bilangan kuat, tentukan bilangan asli terkecil $y$ sehingga $y^{my} + 1$ habis dibagi $2^{m}$. - Diberikan jajaran genjang $ABCD$. Pada sisi luar jajaran genjang tersebut, dikonstruksi persegi-persegi $ABC_{1}D_{1}, BCD_{2}A_{2}, CDA_{3}B_{3}$ dan $DAB_{4}C_{4}$. Pada sisi-sisi luar $B_{4}D_{1}, C_{1}A_{2}, D_{2}B_{3}$, dan $A_{3}C_{4}$ dari segitiga-segitiga $AB_{4}D_{1}, BC_{1}A_{2}, CD_{2}B_{3}$, dan $DA_{3}C_{4}$ dikonstruksi persegi-persegi lain yang berpusat di $O_{A}, O_{B}, O_{C}$ dan $O_{D}$. Buktikan bahwa $$AO_{A} = BO_{B} = CO_{C} = DO_{D}$$.
- Misalkan $A$ suatu himpunan berhingga beranggotakan bilangan asli. Tinjau himpunan-himpunan bagian dari $A$ dengan tiga anggota. Himpunan $A$ dikatakan seimbang apabila banyak himpunan bagian dari $A$ dengan tiga anggota yang jumlah ketiga anggota tersebut habis dibagi 3 sama dengan banyak himpunan bagian dari $A$ dengan tiga anggota yang jumlah ketiga anggota tersebut tidak habis dibagi 3.
1. Berikan satu contoh himpunan seimbang dengan 9 anggota.
2. Buktikan bahwa tidak ada himpunan seimbang dengan 2013 anggota.
Keranjang Belanja
